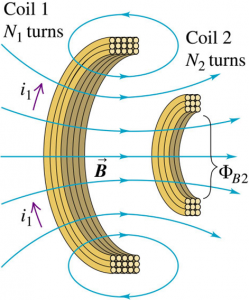
Consider two neighboring coils of wire.
A current $i_{1}$ flowing in coil 1 produces a magnetic field $\vec{B}$ and hence a magnetic flux $\Phi_{B2}$ is produced through each turn of coil 2.
From Faraday’s Law,
$$\epsilon_{2} =-N_{2} \frac{d \Phi_{B2}}{dt}$$
Now, we shall introduce a quantity, mutual inductance to relate the magnetic flux through coil 2 with the current in coil 1.
$$N_{2} \Phi_{B2} = M_{21} i_{1}$$
Hence,
$$\epsilon_{2} =-M_{21} \frac{di_{1}}{dt}$$
The SI unit of mutual inductance: henry
$$\begin{aligned} 1 \, \text{H} &= 1 \, \text{Wb A}^{-1} \\ &= 1 \, \text{V s A}^{-1} \\ &= 1 \Omega \, \text{s} \\ &= 1 \text{J A}^{-2} \end{aligned}$$
Now, consider a changing $i_{2}$ in coil 2 that causes a changing flux $\Phi_{B1}$ and an e.m.f. of $\epsilon_{1}$ in coil 1.
$$\epsilon_{1} =-N_{1} \frac{d \Phi_{B1}}{dt}$$
$$N_{1}\Phi_{B1} = M_{12} i_{2}$$
Hence,
$$\epsilon_{1} =-M_{12} \frac{di_{2}}{dt}$$
It turns out that:
$$\frac{N_{1}\Phi_{B1}}{i_{2}} = M_{12} = M = M_{21} = \frac{N_{2}\Phi_{B2}}{i_{1}} $$
even if the two coils are not symmetric.
Example: Calculating mutual inductance
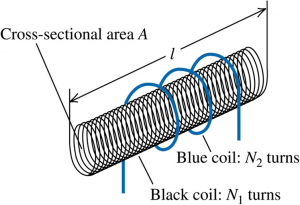
In one form of Tesla coil, a long solenoid with length l and cross-sectional area A is closely wound with $N_{1}$ turns of wire. A coil with $N_{2}$ turns surrounds it at its center. Find the mutual inductance.
$$\begin{aligned} M_{21} &= \frac{N_{2} \Phi_{B2}}{i_{1}} \\ &= \frac{N_{2} \left( B_{1} A \right)}{i_{1}} \\ &= \frac{N_{2}}{i_{1}} \left( \mu_{0} \frac{N_{1}}{l} i_{1} \right) A \\ &= \frac{\mu_{0} N_{1} N_{2} A}{l} \end{aligned}$$
The mutual inductance $M_{21}$ is a constant that depends only on the geometry of the two coils (the size, shape, number of turns, and orientation of each coil and the separation between the coils). If a magnetic material is present, $M_{21}$ also depends on the magnetic properties of the material.
Next: Self-Inductance & Inductors