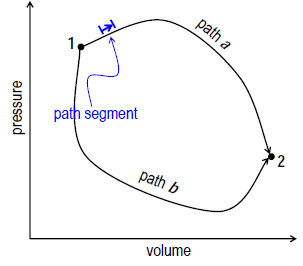
The work output from a system changing from an initial state i to a final state f depends on the path the system takes between these two states.
Consider the following three thought experiment, in which all initial states and all final states of the system are identical and at the same temperature, but the path taken to go from i to f differs:
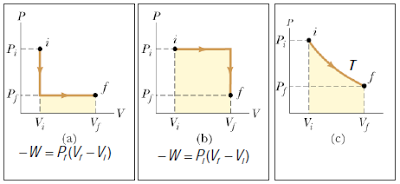 – The work output are also obviously different, because work is given by PdV at each infinitesimal step of the path.
– The work output are also obviously different, because work is given by PdV at each infinitesimal step of the path.
– Thus, work is a path variable – its value does not simply depend on the initial and final states, but on the exact path taken between these two states.
– As a result, it is also not meaningful to write ΔW, because by definition ΔW = W2 – W1, which suggests W depends only on the state.
Path Integrals
Since the work done depends on the path taken, we have to find the infinitesimal work done over an infinitesimal path segment, and integrate over all the segments.
$$W = \int\limits_{1}^{2} dW$$
2. Sum over all the path segments:
– This result depends on the path taken, so W for path a is different from path b.
– Secondly, W for a closed loop is not zero.
Previous: Work output by gas pistons