Circular Motion

Circular motion is a fundamental concept in physics, describing the movement of an object along the circumference of a circle at a constant speed. This motion is omnipresent in the universe, from the rotation of planets in their orbits to electrons circling the nucleus of an atom.

Types of Circular Motion

Uniform Circular Motion: This occurs when an object moves in a circle at a constant speed. The velocity (speed with direction) of the object changes continuously because its direction changes, even though the speed remains constant. This constant change in velocity means the object is undergoing acceleration, known as centripetal acceleration.
Non-Uniform Circular Motion: In this case, an object moves in a circular path with a varying speed, meaning both the magnitude and the direction of the velocity change. This motion involves both centripetal acceleration (towards the center) and tangential acceleration (along the tangent to the path), contributing to the total acceleration of the object.

At the level of ‘A’ Level, we will only focus on uniform circular motion.

Key Concepts in Circular Motion

Angular Velocity ($\omega$): This describes how fast an object rotates or revolves relative to another point, expressed in radians per second (rad/s). The relationship between linear velocity $v$ and angular velocity is $v = \omega \times r$, where $r$ is the radius of the circular path.
Period and Frequency: The period $T$ is the time it takes for one complete revolution around the circle. Frequency $f$ is the number of revolutions per unit time. They are inversely related: $f = \frac{1}{T}$.
Centripetal Force: This is the force required to keep an object moving in a circular path and is directed towards the center of the circle. For uniform circular motion, the centripetal force is responsible for the centripetal acceleration of the object. It can be provided by gravity, tension, friction, or any other force acting perpendicular to the motion of the object.
Centripetal Acceleration: Always directed towards the center of the circle, this acceleration keeps the object moving in a circular path. It is defined as $a_c = \frac{v^2}{r}$, where $v$ is the speed of the object and $r$ is the radius of the circular path.

Radian

For the measurement of angles, you might be used to using degrees (e.g. $360^{\circ}$). Radian is a more convenient unit for the measurement of angles. The concept of a radian provides a more intuitive and universal way to measure angles, moving beyond the traditional degrees.

One radian is the angle subtended at the centre of a circle by an arc of length equal to the radius of the circle.

This definition illuminates the radian as a natural unit for angle measurement, rooted in the geometry of the circle itself.

Radian is given by:

$$\text{Angle (in radians)} = \frac{\text{arc length}}{\text{radius}}\tag{1}$$

The elegance of radians lies in their dimensionless nature (or “no units”), representing a pure ratio of lengths. This quality simplifies many mathematical expressions in physics and engineering, especially those involving rotational motion. To distinguish it from degrees and emphasize its nature, we assign the unit “radian” (rad) to this measure.

For a complete circle, circumference is given by $2 \pi r$, where $r$ is the radius. Using Equation 1, the “angle” of a whole circle can be given by:

$$\begin{aligned} \text{Angle (in radians)} &= \frac{\text{arc length}}{\text{radius}} \\ &= \frac{2 \pi r}{r} \\ &= 2 \pi \end{aligned}$$

This equation equates a full circle to $2 \pi$ radians, establishing a clear relationship between radians and degrees:

$$\begin{aligned} 360^{\circ} &= 2 \pi \\ 1^{\circ} &= \frac{2 \pi}{360} \text{ rad} \\ 57.3^{\circ} &= 1 \text{ rad}\end{aligned}$$

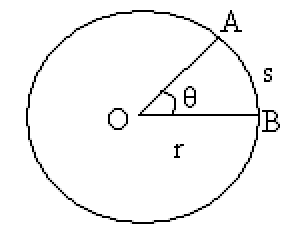
Angular Displacement $\theta$

Angular displacement measures the change in orientation of a body in rotational motion around a fixed point.

This concept is critical in understanding rotational dynamics, providing a direct analog to linear displacement in translational motion. The SI unit of angular displacement is radians, emphasizing its geometric foundation.

Angular displacement, $\theta$ is the angle subtended at centre of a circle by an arc of equal length to the circle’s radius.

Alternative Definition: Angular displacement is the change in angle (measured in radians) of a body as it rotates around a circle.

$$\theta = \frac{s}{r}$$

, where $s$ is the arc length, $r$ is the radius of circle

Angular Velocity $\omega$

Angular velocity, $\omega$ is the rate of change of angular displacement with respect to time.

It quantifies the rate at which an object rotates or revolves,
S.I. unit is $\text{rad s}^{-1}$ or radians per second

$$\begin{aligned} \omega &= \frac{d \theta}{dt} \\ &= \text{or } \frac{\theta}{t} \\ &= \text{or } \frac{\Delta \theta}{\Delta t} \end{aligned}$$

Comparison with Translation Motion

The principles of circular motion closely mirror those of translational motion (normal Kinematics), providing a framework to understand the rotational dynamics through familiar concepts from linear motion:

Translational Motion	Circular Motion
Displacement	Angular Displacement
Velocity	Angular Velocity

This comparison not only highlights the symmetry between linear and rotational phenomena but also enriches our understanding of motion in a comprehensive, unified manner.

Worked Examples

Example 1: Amusement Park

The ‘giant wheel’ at an amusement park provides riders with a journey, making six full rotations within a span of 120 seconds.

1) Compute the angular displacement of the wheel.

2) Determine the average angular velocity throughout the ride.