A storage battery, used for emergency lighting in the even of a power cut operates on 24V. The battery has negligible internal resistance and is rated at 140 ampere-hour.
(a) What is the total energy stored by the battery?
(b) What external resistance would have to be connected to the battery if it were to be discharged in 14 hours?
(c) What power output is the battery giving at this rate of discharge?
= 24 (140 X 3600)
= 12.1 X 106 J(b)
Discharged in 14 hour, I = 140/14
= 10AR = V/I
= 24/10
= 2.4 Ω
(c) P = V2/R
= 242/2.4
= 240 W
The resistivity of the human body is low as compared to the resitivity of the human skin (given as 3.0 X 104 Ω m for dry human skin). For a layer of dry human skin 0.5mm thick, and cross sectional area of 1.0 cm2, determine the resistance of the skin.
=(3.0 X 104)[(0.5 X 10-3)/(1.0 X 10-4)]
= 1.5 X 105Ω
In a particular cathode ray oscilloscope, the measured current of the electron beam is 20.0 µA. How many electrons strike the oscilloscope screen every minute?
I = Q/t
20.0 X 10-6 = Q / 60
Q = 1.20X10-3 CNumber of electrons = (1.20 X 10-3 / 1.602 X 10-19)
= 7.50 X 1015 electrons per minute
The unit of energy commonly used by electrical companies is the kilowatt-hour(kWh).
(a) How many joules are there in a kWh?
(b) A television set rated at 80W is operated from 8pm to midnight. How much energy is this in kWh and in MJ?
= 3.6 X 106J(b)P = 80 X 4
= 320W
= 0.32 kWh
= 0.32(3.6 X 106)
= 1.15 X 106J
A cell of e.m.f. 9.00V and internal resistance of 0.50Ω is connected to a 8.50Ω resistor.
(a) Explain what is meant by an e.m.f. of 9.00V?
Calculate
(b) i) the current in the circuit,
ii) the p.d across the 8.50Ω resistor,
iii) the output efficiency of the circuit
i)
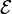 =I(8.50) + I(0.50)
=I(8.50) + I(0.50)I=9/9
I=1Aii)
R=V/I
8.50=V/I
V=8.50Viii)
Efficiency = [8.50/(8.50+0.50)] X 100%
= 94.4%