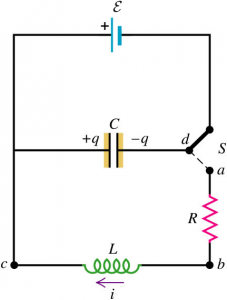
The diagram above shows a L-R-C series circuit. Let’s analyze the circuit:
From Kirchhoff’s loop rule:
$$\begin{aligned} L\frac{di}{dt} + \frac{q}{C} &=-Ri \\ \frac{d^{2}q}{dt^{2}} + \frac{R}{L}\frac{dq}{dt} + \frac{1}{LC}q &= 0 \end{aligned}$$
The equation above resembles the equation for damped simple harmonic motion, whereby:
Overdamped:
$$\frac{R^{2}}{L^{2}} > \frac{4}{LC}$$
Critical damped:
$$\frac{R^{2}}{L^{2}} = \frac{4}{LC}$$
Underdamped:
$$\frac{R^{2}}{L^{2}} < \frac{4}{LC}$$
Solving further:
$$\begin{aligned} q &= Q e^{-\frac{R}{2L}t} \cos{\left( \omega^{\prime} t + \phi \right)} \\ \omega^{\prime} &= \sqrt{\frac{1}{LC}-\frac{R^{2}}{4 L^{2}}} \end{aligned}$$
In the L-R-C circuit, the resistance is the damping mechanism.