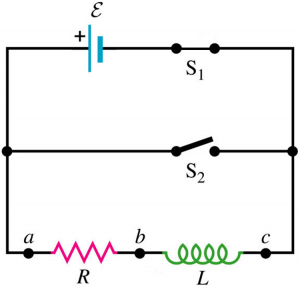
A circuit that includes both a resistor and an inductor, and possibly a source of e.m.f., is called an R-L circuit.
Suppose both switches are open to begin with, and then at some initial time $t = 0$, we close switch $S_{1}$.
Let $i$ be the current at some time $t$ after $S_{1}$ is closed and let $\frac{di}{dt}$ be its rate of change at the time.
From Kirchhoff’s loop rule:
$$E-Ri-L\frac{di}{dt}=0$$
Energy conservation states that:
$$\begin{aligned} iE &= i^{2}R + Li\frac{di}{dt} \\ &= i^{2} +\frac{d}{dt} \left( \frac{1}{2} L i^{2} \right) \end{aligned}$$
Case 1: Initial current through the inductor is 0
$$\begin{aligned} E-Ri-L\frac{di}{dt} &= 0 \\ \frac{di}{dt} &= \frac{E-Ri}{L} \end{aligned}$$
Initially, $i=0$, it follows that:
$$\left( \frac{di}{dt} \right)_{\text{initial}} = \frac{E}{L}$$
In the final state, $\frac{di}{dt} = 0$, it follows that:
$$\left( i \right)_{\text{final}} = I = \frac{E}{R}$$
Using the above relation, we try to solve:
$$\begin{aligned} \frac{di}{dt} &= \frac{E-Ri}{L} \\ \frac{di}{dt} &= R \frac{I-i}{L} \\ \frac{di}{I-i} &= \frac{R}{L} dt \\ \int\limits_{0}^{i} \frac{1}{I-i^{\prime}} \, di^{\prime} &= \frac{R}{L} \int\limits_{0}^{t} \, dt^{\prime} \\ -\ln{\left( I-i^{\prime} \right)}\Big|_{0}^{i} &= \frac{R}{L}t \\ \ln{\left( I-i \right)}-\ln{I} &=-\frac{R}{L}t \\ \ln{\frac{I-i}{I}} =-\frac{R}{L}t \\ I-i &= I e^{-\frac{R}{L}t} \\ i &= I \left[1-e^{-\frac{R}{L}t}\right] \end{aligned}$$
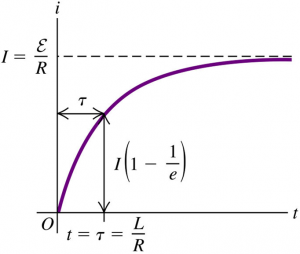The graph above shows the equation obtained above.
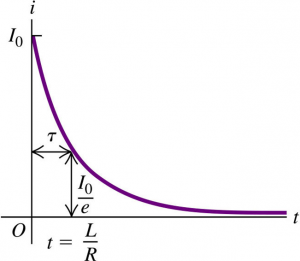
Case 2: Initial current through the inductor is $I_{0}$
From Kirchhoff’s loop rule:
$$\begin{aligned} -Ri-L\frac{di}{dt} &= 0 \\ \frac{di}{dt} &=-\frac{Ri}{L} \end{aligned}$$
Initially, $i=I_{0}$, it follows that:
$$\left( \frac{di}{dt} \right)_{\text{initial}} =-\frac{RI_{0}}{L}$$
In the final state, $\frac{di}{dt} = 0$, it follows that:
$$\left( i \right)_{\text{final}} = 0$$
Using the above relation, we try to solve:
$$\begin{aligned} \frac{di}{dt} &=-\frac{Ri}{L} \\ \frac{di}{i} &=-\frac{R}{L}dt \\ \int\limits_{I_{0}}^{i} \frac{1}{i^{\prime}} \, di^{\prime} &=-\frac{R}{L} \int\limits_{0}^{t} \, dt^{\prime} \\ \ln{i^{\prime}} \Big|_{I_{0}}^{i} &=-\frac{R}{L} t \\ \ln{i}-\ln{I_{0}} &=-\frac{R}{L}t \\ \ln{\frac{i}{I_{0}}} &=-\frac{R}{L}t \\ i &= I_{0}e^{-\frac{R}{L}t} \end{aligned}$$
The graph above shows the equation obtained above.
Next: Phasors & Alternating Currents
Previous: L-R-C Series Circuit
Back To Electromagnetism (UY1)
