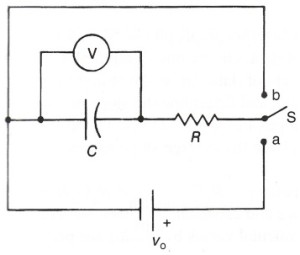
In a RC circuit, the resistor is connected in series with a capacitor. Consider a RC circuit (controlled by a switch) with a power source with emf E, where the resistor has resistance R and capacitance C. Initially, at time t < 0, the switch is open.
$$\begin{aligned} q \, &= 0 \\ i \, &= 0 \end{aligned}$$
At time t = 0, the switch is connected to a.
$$\begin{aligned} q \, &= 0 \\ i \, &= \frac{E}{R} = I_{0} \end{aligned}$$
At time t > 0,
$$\begin{aligned} v_{bc} \, &= \frac{q}{C} \\ v_{ab} \, &= iR \end{aligned}$$
Since $E-iR-\frac{q}{C} = 0$, we have $i = \frac{E}{R} – \frac{q}{RC}$.
Charging a capacitor
We are interested to find out how the charge in the capacitor of the RC circuit changes with time as it is charged. In order to do that, we can perform integration on the equation above.
$$\begin{aligned} i \, &= \frac{E}{R} – \frac{Q}{RC} \\ \frac{dq}{dt} &= \frac{CE-q}{RC} \\ \frac{dq}{CE-q} &= \frac{1}{RC} \, dt \\ \int\limits_{0}^{q} \frac{dq’}{CE-q’} &= \frac{1}{RC} \int\limits_{0}^{t} dt’ \\ -\text{ln} \, (CE-q’) \left. \right|_{0}^{q} &= \frac{t}{RC} \\ \text{ln} \, \left( \frac{CE-q}{CE} \right) &=-\frac{t}{RC} \\ \text{ln} \, (CE-q)-\text{ln} \, (CE) &=-\frac{t}{RC} \\ CE-q \, &= CEe^{-\frac{t}{RC}} \\ q \, &= CE\left[1-e^{-\frac{t}{RC}} \right]\end{aligned}$$
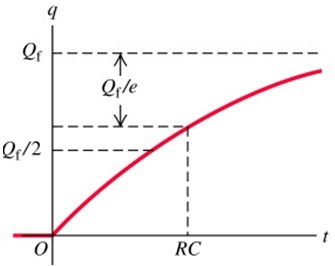
$$Q = Q_{f}\left[1-e^{-\frac{t}{RC}} \right]$$
The quantity $\tau = RC$ is called the time constant of the circuit. When $t = \tau$, the charge in the capacitor is $\left( 1-\frac{1}{e} \right)Q_{f} = 0.63Q_{f}$, where $Q_{f}$ is the amount of charge stored in the capacitor when it is full. The graph below shows the changes in charge stored in capacitor with time.
We can find the equation of current with time by differentiating the equation for charge with time. (Since $I = \frac{dq}{dt}$)
$$i = i_{0} e^{-\frac{t}{RC}}$$
Discharging the capacitor
Consider a RC circuit (with no power source and controlled by a switch). Initially, at time t < 0, the capacitor holds a charge of $Q_{0}$.
$$\begin{aligned} q \, &=Q_{0} \\ i \, &= 0 \end{aligned}$$
Then at time t = 0, the switch is connected to b and the capacitor begins to discharge.
$$\begin{aligned} q \, &= Q_{0} \\ i \, &= -\frac{Q_{0}}{RC} = I_{0} \end{aligned}$$
At time t > 0,
$$\begin{aligned} v_{bc} \, &= \frac{q}{C} \\ v_{ab} \, &= iR \end{aligned}$$
From the two equations above, we have $-iR-\frac{q}{C} = 0$ which will lead to $i =-\frac{q}{RC}$.
We are interested to find out how the charge in the capacitor of the RC circuit changes with time as it is discharged. In order to do that, we can perform integration on the equation above.
$$\begin{aligned} i \, &=-\frac{q}{RC} \\ \frac{dq}{dt} &=-\frac{q}{RC} \\ \frac{dq}{q} &=-\frac{1}{RC} \, dt \\ \int\limits_{Q_{0}}^{q} \frac{dq’}{q’} &=-\frac{1}{RC} \int\limits_{0}^{q} \, dt’ \\ \text{ln} \, q’ \left. \right|_{Q_{0}}^{q} &=-\frac{t}{RC} \\ \text{ln} \, \left(\frac{q}{Q_{0}} \right) &=-\frac{t}{RC} \\ \text{ln} \, q -\text{ln} \, Q_{0} &=-\frac{t}{RC} \\ q \, &= Q_{0}e^{-\frac{t}{RC}} \end{aligned}$$
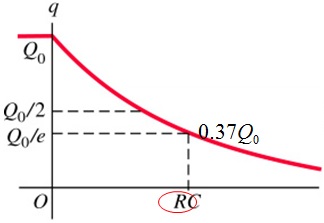
Similar to the charging case, the time constant is $\tau = RC$, which is the time taken for the charge to drop to $\frac{Q_{0}}{e} \approx 0.37 Q_{0}$.
We can find the equation of current with time by differentiating the equation for charge with time. (Since $I = \frac{dq}{dt}$)
$$i = I_{0} e^{-\frac{t}{RC}}$$
where $I_{0} = -\frac{Q_{0}}{RC}$
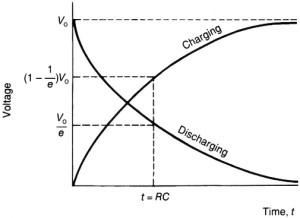
Since the voltage across the capacitor is closely tied to the current charge held by the capacitor, you will obtain the graph above for charging and discharging.
Next: Magnetic Field & Motion Of Charged Particles In Magnetic Fields