Any device that supplies a sinusoidally varying voltage (potential difference)
$$v = V \cos{\omega t}$$
, where V is the voltage amplitude,
or current
$$i = I \cos{\omega t}$$
, where I is the current amplitude,
is an alternating current (ac) source with angular frequency:
$$\begin{aligned} \omega &= 2 \pi f \\ &= \frac{2 \pi}{T} \end{aligned}$$
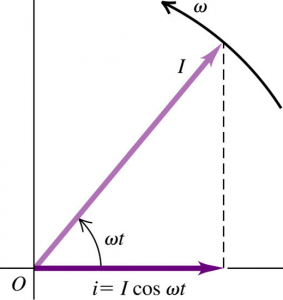
You can represent the information in a Phasor diagram, as shown below.
Finding the root-mean-square value for the alternating current:
$$\begin{aligned} i^{2} &= I^{2} \cos^{2}{\omega t} \\ i^{2} &= \frac{1}{2} I^{2} \left( 1 + \cos{2 \omega t} \right) \\ \frac{1}{T} \int\limits_{0}^{T} i^{2} \, dt &= \frac{1}{2} I^{2} \\ I_{\text{rms}} &= \frac{1}{\sqrt{2}} I \end{aligned}$$
A diode (rectifier) is a device that conducts better in one direction than in the other – an ideal diode has zero resistance for one direction of current and infinite resistance for the other.
For a full-wave rectifier circuit, the rectified average current is given by:
$$\begin{aligned} I_{rav} &= \frac{2}{T} \int\limits_{0}^{\frac{T}{2}} I \sin{\omega t} \, dt \\ &= \frac{4I}{\omega T} \\ &= \frac{2}{\pi} I \end{aligned}$$