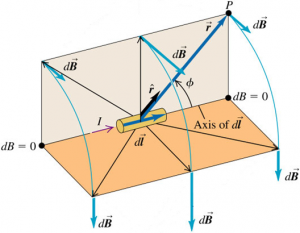
The magnetic field caused by a short segment $d\vec{l}$ of a current-carrying conductor can be obtained by a short derivation:
We know that the magnetic field of a single point charge q moving with a constant velocity $\vec{v}$ is given by:
$$B = \frac{\mu_{0}}{4 \pi} \frac{|q|v\sin{\phi}}{r^{2}}$$
Hence,
$$dB = \frac{\mu_{0}}{4 \pi} \frac{|dQ|v_{d}\sin{\phi}}{r^{2}}$$
, where dQ is the element of charge in the short segment of current-carrying conductor and $v_{d}$ is the drift velocity of the charge carriers in the conductor.
We need to calculate dQ:
$$|dQ| = n \times A \, dl \times |q|$$
We know that:
$$I = n |q| v_{d} A$$
, where n is the number of charge carriers per unit volume
Hence,
$$dB = \frac{\mu_{0}}{4 \pi} \frac{I \, dl \, \sin{\phi}}{r^{2}}$$
OR
$$d\vec{B} = \frac{\mu_{0}}{4 \pi} \frac{I}{r^{2}} d\vec{l}\times \hat{r}$$
The above equation is known as Biot-Savart Law.
The Principle of superposition of magnetic fields states that the total magnetic field caused by several moving charges is the vector sum of the fields caused by the individual charges.
The total magnetic field at any point in space due to the current in a complete circuit will be:
$$\vec{B} = \frac{\mu_{0}}{4 \pi} \int \frac{I}{r^{2}} \, d\vec{l} \times \hat{r}$$
Next: Magnetic Field Of A Straight Current Carrying Conductor