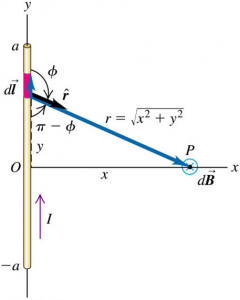
Consider a straight conductor with length 2a carrying a current I. Find the magnetic field at point P which is located at a distance x from the conductor on its perpendicular bisector.
From Biot-Savart Law, we have:
$$\vec{B} = \frac{\mu_{0}}{4 \pi} \int \frac{I}{r^{2}} \, d\vec{l} \times \hat{r}$$
First, we will need to work out what is $d\vec{l} \times \hat{r}$.
$$d\vec{l} = dl \, \hat{j}$$
$$\begin{aligned} \hat{r} &= \cos{\left( \phi-90^{\circ} \right)}\hat{i} – \sin{\left( \phi-90^{\circ}\right)}\hat{j} \\ &= \sin{\phi} \hat{i} + \cos{\phi} \hat{j} \end{aligned}$$
Hence,
$$d\vec{l} \times \hat{r} = \, – \sin{\phi} \, dl \, \hat{k}$$
Substituting that into the Biot-Savart Law, we have:
$$\vec{B} = \left[ \frac{\mu_{0}I}{4 \pi} \int \frac{1}{r^{2}} \left( – \sin{\phi} \, dl \right) \right] \hat{k}$$
Notice that both $r^{2}$ and $\sin{\phi}$ can be replaced with:
$$r^{2} = x^{2} + y^{2}$$
$$\sin{\phi} = \frac{x}{\sqrt{x^{2}+y^{2}}}$$
We have:
$$\begin{aligned} \vec{B} &= \left[ \frac{\mu_{0}I}{4 \pi} \int\limits_{-a}^{a} \frac{1}{x^{2} + y^{2}} \left( – \frac{x}{\sqrt{x^{2}+y^{2}}} \, dy \right) \right] \hat{k} \\ &= -\frac{\mu_{0}I}{4 \pi} \int\limits_{-a}^{a} \frac{x \, dy}{\left(x^{2}+y^{2} \right)^{\frac{3}{2}}} \hat{k} \\ &= -\frac{\mu_{0}I}{4 \pi} \frac{2a}{x \sqrt{x^{2}+a^{2}}} \hat{k} \end{aligned}$$
The magnitude of the magnetic field is:
$$B = \frac{\mu_{0}I}{4 \pi} \frac{2a}{x \sqrt{x^{2}+a^{2}}}$$
What if the current carrying conductor is long (assumed to be infinite in length)?
From the above equation, we have:
$$\begin{aligned} B &= \frac{\mu_{0}I}{4 \pi} \frac{2a}{x \sqrt{x^{2}+a^{2}}} \\ &= \frac{\mu_{0}I}{2 \pi} \frac{1}{x \sqrt{1 + \frac{x^{2}}{a^{2}}}} \end{aligned}$$
For infinite length of wire, $a \rightarrow \infty$, $\frac{x^{2}}{a^{2}} \rightarrow \infty$. We have:
$$B = \frac{\mu_{0}I}{2 \pi x}$$
x is normally denoted by r, which is the distance from the conductor to the point.
Hence,
$$B = \frac{\mu_{0}I}{2 \pi r}$$
Next: Magnetic Field & Force Between Parallel Conductors