UY1: Magnetic Field & Force Between Parallel Conductors

This page gives the UY1 working model/result for Magnetic Field & Force Between Parallel Conductors. You reuse it when you build fields/potentials by symmetry or superposition, and when you connect fields to forces, energy, and circuits.

Module path: Electromagnetism (UY1)
Practice: UY1 Electromagnetism Quiz
Full routing: UY1 Assessment Map
Math toolkit: Mathematics for Undergraduate Physics

1) At a glance

Field from wire 1 at wire 2:

B₁ = μ₀ I₁/2π d

Force per unit length on wire 2:

F/L = I₂B₁ = μ₀ I₁I₂/2π d

Same-direction currents attract; opposite-direction currents repel.
Modelling context: this is the long straight wire approximation (end effects neglected) and magnetostatics (steady currents).

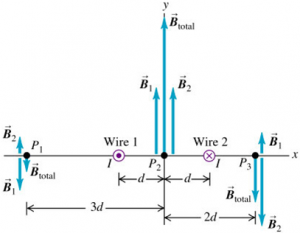
Prerequisites: Magnetic Field Of A Straight Current Carrying Conductor, Magnetic Force On A Current Carrying Conductor

2) Setup

Two long straight parallel wires separated by distance d, carrying currents I₁ and I₂.

Use long-wire approximation.
Field from each wire is circular around that wire.
Force direction from vecF = IvecL × vecB.

Use the right-hand grip rule to get vec B₁ direction around wire 1 at the location of wire 2.
Then use vec F₂ = I₂vec L × vec B₁ to get the force direction on wire 2.
Same-direction currents attract is a good final sense-check, but derive it once with cross products so you trust the rule.

3) Core derivation/explanation

At wire 2, wire 1 creates

B₁ = μ₀ I₁/2π d.

Then magnetic force on length L of wire 2:

F = I₂LB₁.

Hence

F/L = μ₀ I₁I₂/2π d.

By symmetry, the same magnitude acts on wire 1 in opposite direction (Newton’s third law).

Direction result:

Currents in same direction pull wires together.
Opposite directions push wires apart.

Checks (sanity)

If either current is zero, force is zero.
Doubling separation d halves F/L.

4) Worked example(s)

Two wires carry I₁ = 10 A and I₂ = 15 A, separated by d = 5.0 cm.

F/L = μ₀ I₁I₂/2π d = (4π × 10⁻⁷)(10)(15)/2π(5.0 × 10⁻²) = 6.0 × 10⁻⁴ N m⁻¹.

If currents are same direction, this is attractive.

5) Practice set (with hints + answers)

If separation d doubles, what happens to F/L?
Wires carry equal currents in opposite directions. Is force attractive or repulsive?
Compute F/L for I₁ = I₂ = 20 A and d = 0.20 m.

Hints

Use inverse proportionality in d.
Use current-direction rule.
Substitute directly into μ₀ I₁I₂/(2π d).

Answers

It halves.
Repulsive.
F/L = 4.0 × 10⁻⁴ N m⁻¹.

6) Summary + next steps

Parallel currents interact through each other’s magnetic fields.
The force law is simple but direction-sensitive.
This interaction underlies the historical SI definition of current.

Next: Magnetic Field Of A Circular Current Loop Previous: Magnetic Field Of A Straight Current Carrying Conductor Back To Electromagnetism