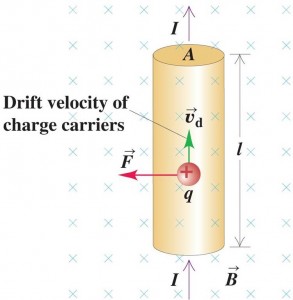
Consider a straight segment of a conducting wire, with length $l$ and cross-sectional area $A$. The wire is in a uniform magnetic field $\vec{B}$, which is perpendicular to the plane of the diagram and directed into the plane.
Average magnetic force on each charge is given by:
$$\begin{aligned} \vec{F} &= q \vec{v}_{d} \times \vec{B} \\ F &= qv_{d}B \end{aligned}$$
Total magnetic force on all the moving charges is given by: (n is the no. of charge carriers per unit volume)
$$\begin{aligned} F &= \text{Total no. of electrons} \times qv_{d}B \\ &= nAl \times qv_{d}B \\ &= nqv_{d}A \times lB \end{aligned}$$
Recall that: $J = \frac{I}{A} = nqv_{d}$ which gives $I = nqv_{d}A$.
Hence,
$$F = IlB$$
If the $\vec{B}$ field is not perpendicular to the wire but makes an angle $\phi$ with it,
$$\begin{aligned} F &= IlB_{\perp} \\ &= IlB \sin{\phi} \end{aligned}$$
The general form will be:
$$\vec{F} = I \vec{l} \times \vec{B}$$
Magnetic force on an infinitesimal wire section will be:
$$d\vec{F} = I \, d\vec{l} \times \vec{B}$$