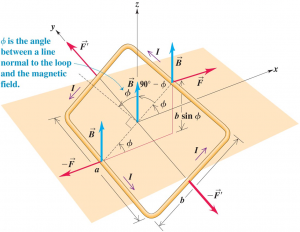
Consider a rectangular loop of wire with side lengths a and b, in a uniform magnetic field $\vec{B}$. The loop carries a current I.
The magnetic field is given by:
$$\vec{B} = B \hat{k}$$
Recall that the magnetic force is given by:
$$\vec{F} = I \vec{l} \times \vec{B}$$
Hence, the magnetic force on the straight segment on the right of the diagram above is given by:
$$\begin{aligned} \vec{F} &= I \vec{l} \times \vec{B} \\ &= I a \hat{j} \times B \hat{k} \\ &= IaB \hat{i} \end{aligned}$$
The magnetic force on the other straight segment will just be $-\vec{F}$ because the direction of the current flow is just opposite that of the right segment.
There is two other force on the current loop: the two short segment of the current loop. The magnitude of the force will be:
$$F’ = IbB\cos{\phi}$$
or
$$F’ = IbB\sin{90^{\circ}-\phi}$$
Since $\vec{F’}$ and $-\vec{F’}$ are of the same magnitude with opposite direction, they produce no net acceleration.
The net torque is solely produced by $\vec{F}$ and $-\vec{F}$, which is given by:
$$\begin{aligned}\tau &= \perp \, \text{dist} \times \, \text{force} \\ &= b\sin{\phi} \times IaB \\ &= IAB\sin{\phi} \end{aligned}$$
We notice that the result obtained above can be written as:
$$\vec{\tau} = I \vec{A} \times \vec{B}$$
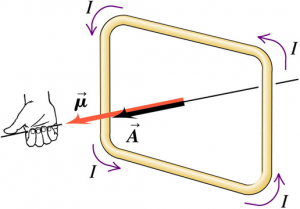
It is known that $I\vec{A}$ correspond to a quantity known as magnetic dipole moment or magnetic moment. Right hand rule can be used to determine the direction of the magnetic dipole moment.
$$\vec{\mu} = I \vec{A}$$
Hence,
$$\vec{\tau} = \vec{\mu} \times \vec{B}$$
A magnetic moment in an externally produced magnetic field has a potential energy U:
$$U = – \vec{\mu} . \vec{B}$$
A current loop, or any other body that experiences a magnetic torque is called a magnetic dipole.
When a magnetic dipole changes orientation in $\vec{B}$, $\vec{B}$ does work on it:
$$\begin{aligned} dW &= – \tau \, d\phi \\ &= – \mu B \sin{\phi} \, d\phi \\ W &= \int\limits_{\phi_{1}}^{\phi_{2}} – \mu B \sin{\phi} \, d\phi \\ &= \mu B \cos{\phi_{2}} – \mu B \cos{\phi_{1}} \end{aligned}$$
In a motor, a magnetic torque acts on a current-carrying conductor, and electrical energy is converted to mechanical energy.
All the above relations for magnetic moment are valid for a plane current loop of any shape. This is because any wire loop of arbitrary shape can always be decomposed into rectangular loops.
Next: Magnetic Field Lines & Magnetic Flux
Previous: Magnetic Force On A Curved Conductor
Back To Electromagnetism (UY1)