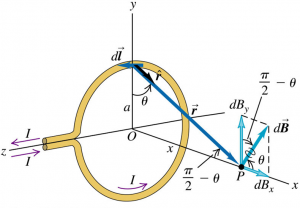
Consider a circular conductor with radius a that carries a current I. Find the magnetic field at point P on the axis of the loop, at a distance x from the center.
From Biot-Savart Law:
$$\vec{B} = \frac{\mu_{0}}{4\pi} \int \frac{I}{r^{2}} \, d\vec{l} \times \hat{r}$$
Due to the symmetry of the current loop, the $\vec{B_{y}}$ at point P due to the top half of the current loop will cancel out the $\vec{B_{y}}$ due to the lower half of the current loop. Hence, we will only need $\vec{B_{x}}$.
$$dB_{x} = \frac{\mu_{0}}{4\pi} \frac{I}{x^{2}+a^{2}} \, dl \, \cos{\theta}$$
From the diagram,
$$\begin{aligned} \cos{\theta} &= \frac{a}{r} \\ &= \frac{a}{\sqrt{x^{a}+a^{a}}} \end{aligned}$$
Hence,
$$\begin{aligned} B_{x} &= \frac{\mu_{0}Ia}{4 \pi \left( x^{2} + a^{2} \right)^{\frac{3}{2}}} \int\limits_{0}^{2 \pi a} \, dl \\ &= \frac{\mu_{0}Ia^{2}}{2 \left( x^{2} + a^{2} \right)^{\frac{3}{2}}} \end{aligned}$$
If there are a coil consisting of N loops, all with the same radius,
$$B_{x} = \frac{\mu_{0}NIa^{2}}{2 \left( x^{2} + a^{2} \right)^{\frac{3}{2}}}$$
Note that the answer above assumes that the loops have no thickness.
From the equation above, it is obvious that the maximum $B_{x}$ will be at $x = 0$.
$$B_{max} = \frac{\mu_{0} N I}{2a}$$
Alternatively, you can set $\frac{dB_{x}}{dx} = 0$.
$$\frac{dB_{x}}{dx} = \, – \frac{3 \mu_{0} NIa^{2}x}{2 \left( x^{2} + a^{2} \right)^{\frac{5}{2}}} = 0$$
Previous: Magnetic Field & Force Between Parallel Conductors