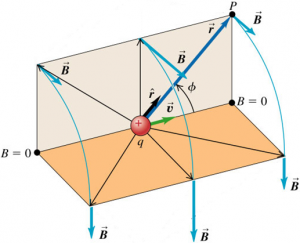
The magnetic field of a single point charge q moving with a constant velocity $\vec{v}$ is given by:
$$\vec{B} = \frac{\mu_{0}}{4 \pi} \frac{q}{r^{2}} \vec{v} \times \hat{r}$$
OR
$$B = \frac{\mu_{0}}{4 \pi} \frac{|q|v\sin{\phi}}{r^{2}}$$
,where $\mu_{0} = 4 \pi \times 10^{-7} \, \text{T m A}^{-1}$
The direction of $\vec{B}$ is perpendicular to the plane containing the line from source point to field point $P$ and the particle velocity vector $\vec{v}$.
For a point charge moving with velocity $\vec{v}$, the magnetic field lines are circles centered on the line of $\vec{v}$ and lying in planes perpendicular to this line.
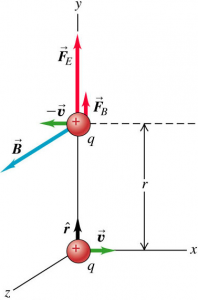
Example: Forces Between Two Moving Protons
Two protons move parallel to the x-axis in opposite direction at the same speed v. At the instant shown, find the electric and magnetic forces on the upper proton and determine the ratio of their magnitudes.
There are two kinds of forces experienced by the protons: electric force and magnetic force ($\vec{B}$ field from the moving charges).
The electric force experienced by the upper proton is given by:
$$\vec{F}_{E} = \frac{1}{4 \pi \epsilon_{0}} \frac{q^{2}}{r^{2}} \hat{j}$$
The magnetic field generated by the lower proton at the position of the upper proton is given by:
$$\begin{aligned} \vec{B} &= \frac{\mu_{0}}{4 \pi} \frac{q}{r^{2}} v \hat{i} \times \hat{j} \\ &= \frac{\mu_{0}}{4 \pi} \frac{qv}{r^{2}} \hat{k} \end{aligned}$$
The magnetic force experienced by the upper proton due to the magnetic field generated by the lower proton will be given by:
$$\begin{aligned} \vec{F}_{B} &= q \left(-v \hat{i} \right) \times B \hat{k} \\ &= qvB \hat{j} \\ &= \frac{mu_{0}}{4 \pi} \frac{q^{2}v^{2}}{r^{2}} \hat{j} \end{aligned}$$
Now, we shall calculate the ratio of their magnitudes:
$$\begin{aligned} \frac{F_{B}}{F_{E}} &= \epsilon_{0} \mu_{0} v^{2} \\ &= \frac{v^{2}}{c^{2}} \end{aligned}$$
The last simplification is due to this relation: $\epsilon_{0} \mu_{0} = \frac{1}{c^{2}}$.
Next: Magnetic Field Of A Current Element