An oscillation is damped when the amplitude and mechanical energy of a system gradually decreases to zero as a result of dissipative forces.(air resistance, friction, internal forces)
Amplitude and frequency will be reduced during damping.
Damping is the process whereby energy is taken from the oscillating system.
When there is damping, amplitude decrease and period increase.
Types of Damping
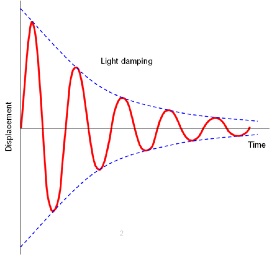
1. Light damping
- Defined oscillations are observed, but the amplitude of oscillation is reduced gradually with time.
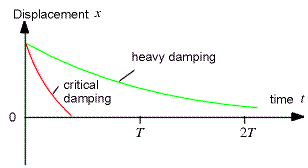
2. Critical Damping
- The system returns to its equilibrium position in the shortest possible time without any oscillation.
3. Heavy Damping
- The system returns to the equilibrium position very slowly, without any oscillation. Heavy damping occurs when the resistive forces exceed those of critical damping.
Critical Damping is important so as to prevent a large number of oscillations and there being too long a time when the system cannot respond to further disturbances.
- Instruments such as balances and electrical meters are critically damped so that the pointer moves quickly to the correct position without oscillating.
- The shock absorbers on a car critically damp the suspension of the vehicle and so resist the setting up of vibration wich could make control difficult or cause damage.
The heavy is wrong, not impressed looked a fool in my physics lesson
I agree with physics kid . I’m not angry I’m just disappointed. You have really let yourselves down.
Heavy damping: large dissipative force, no oscillations occur and the system returns very slowly to equilibrium position
Why does time changes for heavy damping but not for critical damping
Hi All,
I’ve a strange (possible slightly sad!) application. Imagine, if you can, I’m a guy who likes making big model tanks. The tank turret has a Action Man sized figure poking out of the turret (top half from the waist up). When the tank moves it bounces (slightly) up and down but rocks back and forth and side to side as it drives over rough ground ( + pitching and yawing). I can imagine fixing my figure to a gimbal at its waist with a mass (a few 10s of grams?) slung underneath to maintain stability when the tank moves around. To more accurately simulate the action of a real human tank commander in a real tank (with stomach muscles!) I need to critically damp (to human timescalesscale!!) the oscillations arising in the figure from the tank’s movement. This is a low mass (10’s of grams), low frequency (0.1 – 5sec) random movements over low angles (normally <10 degrees from horizontal).
Can anyone think how I might critically (or even over-)damp (three dimensionally) the upper half of a gimbal mounted (even rubber band mounted) relatively low mass system without resorting to viscosity damped liquid piston or electrically actuated drives to achieve this.
As you will have realised, I'm no engineer, but having worked with you guys before, I'm constantly surprised about the degree of imagination you can apply to such simple problems.
Any thoughts would be very gratefully received given there are a frightening number of us sad characters who might me interested in such an innovation.
Thanks for you help
Bob
dont be like bob guys..
Why time period and frequency changes for heavy damping but not for critical damping?
During heavy/critical damping, there are no oscillations.
i am a bit confused as to why frequency decreases during damping?
Because you are taking energy out from the system. Hence, there might not be enough energy in the system to sustain it’s original frequency.