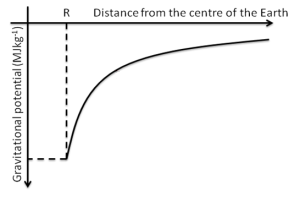
Gravitational Potential & Gravitational Potential Energy

1. Definitions (Must Know)

A. Gravitational potential, φ

Gravitational potential, φ, at a point is the work done per unit mass by an external force in bringing a small test mass from infinity to that point (slowly, so its kinetic energy does not change).

For a point mass M:

φ = -GM/r

Unit: J kg⁻¹.

B. Reference level (zero at infinity)

By convention, φ = 0 at infinity. Since gravity is attractive, φ is negative everywhere in the field of an isolated mass.

Scroll diagram horizontally to read all labels.

Data table

φ = −GM/r (scaled)
Distance from Earth's centre, r (10⁷ m)	Potential, φ (10⁷ J kg⁻¹)
1	-6
1	-4
2	-2
4	-1

C. Gravitational potential energy, U

Gravitational potential energy of a mass m at a point is:

U = mφ = -GMm/r

It is the energy of the two-body system (M and m) relative to zero at infinity.

D. Potential difference and work done

The potential difference between points A and B is:

Δφ = φB-φA

For slow movement (no change in kinetic energy), the work done by the external force is:

Wₑₓₜ = mΔφ = Δ U

2. Key Ideas (What Earns Marks)

• φ is energy per unit mass (J kg⁻¹); U is energy (J).
• For an isolated mass with φ = 0 at infinity, φ is negative at finite r; “higher potential” means “less negative”.
• For a point mass: φ = -GM/r, U = -GMm/r
• Field strength and potential are linked (syllabus): gᵣ = -dφ/dr
• Moving to a higher orbit requires energy: r increases, φ increases (becomes less negative), so Δ U>0.

3. Detailed Explanations

A. Why φ is negative

Using the definition with φ = 0 at infinity:

• Gravity pulls the test mass inward.
• To move the test mass slowly inward, the external force must act outward (opposite the displacement).
• So the external force does negative work. Therefore φ is negative.

Equivalently: a bound system has U lt 0 relative to infinity, so φ = U/m lt 0.

B. Using potential to calculate energy changes

1. Find φ at each position using φ = -GM/r.
2. Compute Δφ = φB-φA.
3. Multiply by mass to get energy change: Δ U = mΔφ.

If the object is moved slowly, Wₑₓₜ = Δ U.

C. Potential gradient (link to field strength)

Choose the outward radial direction as positive. The radial component of gravitational field strength is then

gᵣ = -dφ/dr.

If r is measured positive outward from the centre, then vecg points inward, so it has a negative radial sign.

From φ = -GM/r:

dφ/dr = + GM/r² Rightarrow gᵣ = -GM/r².

So the magnitude of the field strength is:

|vecg| = GM/r²

Near Earth’s surface (uniform field model), the potential change over a small height change Δ h is approximately:

Δφ ≈ g Δ h

so Δ U ≈ mg Δ h.

D. Equipotential surfaces

An equipotential surface is a surface where φ is constant.

• Moving along an equipotential: Δφ = 0 Rightarrow Δ U = 0 Rightarrow Wₑₓₜ = 0.
• Gravitational field lines are perpendicular to equipotential surfaces.
• Work done by gravity is Wg = -Δ U = -mΔφ.

4. Common Mistakes

• Missing the negative sign in φ = -GM/r or U = -GMm/r.
• Using radius/altitude wrongly: r is centre-to-centre; for altitude h, r = RE + h.
• Confusing φ (per unit mass) with U (total energy).
• Forgetting that “increase in potential” can mean “less negative”.

5. Exam Tips

• State the reference: “φ = 0 at infinity”.
• If the question asks for energy required to raise orbit: use Δ U = m(φ₂-φ₁) and expect Δ U>0.
• If you use gᵣ = -dφ/dr, define outward as positive so the negative radial component means inward.

6. Worked Examples

Example 1: Gravitational potential at a given rCore

Find the gravitational potential at a point 1.00 × 10⁷ m from Earth’s centre. Take ME = 5.97 × 10²⁴ kg.

Show answer

φ = -GM/r; = -(6.67 × 10⁻¹¹)5.97 × 10²⁴/1.00 × 10⁷; ≈ -3.98 × 10⁷ J kg⁻¹

Example 2: Potential energy from U = mφCore

A 1000 kg satellite is at r = 1.00 × 10⁷ m from Earth’s centre. Find its gravitational potential energy (relative to infinity).

Show answer

Using φ ≈ -3.98 × 10⁷ J kg⁻¹ from Example 1:

U = mφ; = (1000)(-3.98 × 10⁷); ≈ -3.98 × 10¹⁰ J

Example 3: Energy needed to raise a satellite’s orbitCore

A 700 kg satellite moves from altitude 200 km to 1000 km above Earth. Take RE = 6.37 × 10⁶ m and GME = 3.99 × 10¹⁴ m³ s⁻². Estimate the work done by an external force if the satellite is raised slowly.

Show answer

r₁ = RE + 2.00 × 10⁵ = 6.57 × 10⁶ m r₂ = RE + 1.00 × 10⁶ = 7.37 × 10⁶ m

Δφ = φ₂-φ₁; = -GM/r₂-(-GM/r₁); = GM(1/r₁-1/r₂); ≈ (3.99 × 10¹⁴)(1/6.57 × 10⁶-1/7.37 × 10⁶); ≈ 6.6 × 10⁶ J kg⁻¹

Wₑₓₜ = mΔφ; ≈ (700)(6.6 × 10⁶); ≈ 4.6 × 10⁹ J

Example 4: Using gᵣ = -dφ/drCore

At a distance r = 4.20 × 10⁷ m from Earth’s centre, estimate the magnitude of gravitational field strength. Take GME = 3.99 × 10¹⁴ m³ s⁻².

Show answer

|vecg| = GM/r² = 3.99 × 10¹⁴/(4.20 × 10⁷)² ≈ 0.23 N kg⁻¹

Example 5: Potential difference and energy change between two radiiCore

Two satellites of the same mass move between radii r₁ and r₂ around the same planet.

1. Write an expression for Δ φ = φ₂ - φ₁ in terms of GM, r₁, and r₂.
2. Hence write an expression for the change in gravitational potential energy Δ U for a satellite of mass m.

Show answer

Using φ = -dfracGMr: Δφ = φ₂-φ₁ = -GM/r₂-(-GM/r₁) = GM(1/r₁-1/r₂)

Then: Δ U = mΔφ = mGM(1/r₁-1/r₂)

7. Mind Stretchers

Mind stretcher 1: Radius when potential is halvedExtension

At what radius is the gravitational potential half (same sign) of its value at radius r? (Express your answer in terms of r.)

Show answer

Since φ = -GM/r:

φ'/φ = -GM/r'/-GM/r = r/r'

For φ' = tfrac12φ, we need r/r' = 1/2, so r' = 2r.

Mind stretcher 2: Why U stays constant in a circular orbitExtension

Explain why an object in circular orbit has constant gravitational potential energy even though a gravitational force acts on it.

Show answer

For a circular orbit, r is constant, so φ = -GM/r and U = mφ are constant.

Also, gravity points towards the centre while the instantaneous displacement is tangential, so the gravitational force does no work on the object in uniform circular motion.

Mind stretcher 3: Optional (Enrichment)Extension

A. Force as a potential gradient (calculus form)

Sometimes you will see:

Fᵣ = -dU/dr

This is the radial component of the gravitational force derived from how U changes with r. For A Level, the key examinable gradient relationship is gᵣ = -dφ/dr when outward is positive.

8. Practice, Quiz and Next Step

Close your notes and use Gravitational Potential & Gravitational Potential Energy in the supplied context below. This requires a constructed explanation or working, not recognition of an option.

Fresh context: An unfamiliar data set or physical system requires you to apply Gravitational Potential & Gravitational Potential Energy while stating the model, regime and assumptions.

1. Retrieve: define gravitational potential & gravitational potential energy in your own words, including units, sign or conditions where relevant.
2. Represent: Choose and label an appropriate diagram, graph, table or symbolic model; derive or justify the relationship used.
3. Apply: Reach a conclusion, then evaluate it using units, uncertainty, a limiting case and one practical or modelling limitation.

Check the response before looking back

• The model, regime, coordinates and assumptions are explicit.
• The derivation or multi-step reasoning is visible rather than implied.
• The conclusion is tested against units, data quality and a limiting case.
• A practical control, uncertainty or model limitation is evaluated where applicable.

If one check fails, name that exact gap, revisit the matching explanation or worked example, and redo the task with different values or a different situation. Then use theA-Level Physics course hub orpractice browser for an independent re-test.