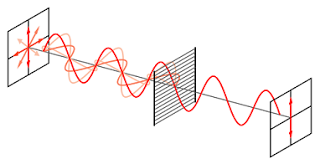
An ordinary light source consists of a large number of randomly oriented atomic emitters. Each excited atom radiates a polarized wavetrain for roughly $10^{-8}$ s. New wave trains are constantly emitted and the overall polarization changes rapidly in a completely unpredictable fashion. Therefore natural light should not be called unpolarized light. It should be randomly polarized light.
A polarizer is an optical device whose input is natural light and the output is of some form of polarized light.
When randomly polarized light passes through a plane polarizer, the emergent polarized light will have an intensity which is halved the original light.
2 plane polarisers:
When a plane polarized light passes through another plane polarizer at another angle, the intensity of the light that exits is given by:
$I_{\theta} = I_{o} \text{sin}^{2} \, \theta$, where
θ is the angle between the transmission axis of the 1st polariser and that of the anaylzer.
Io being the intensity of light passing through the 1st polarizer.
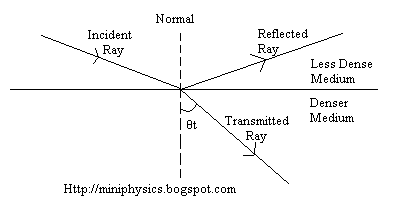
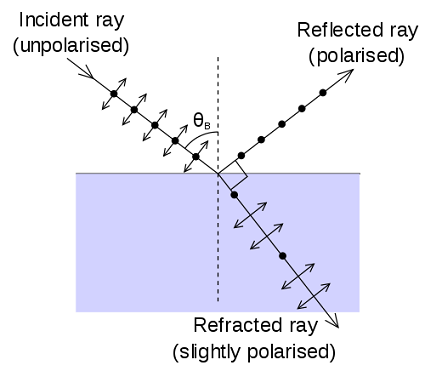
Polarization By Reflection
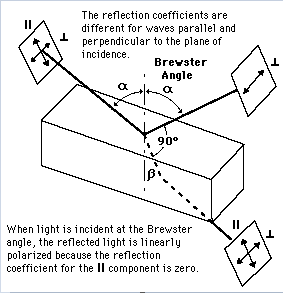
At a particular angle of incidence, such that the angle of reflection and the angle of transmission adds up to 90°, the reflected ray will be polarised in the direction parallel to the surface, perpendicular to the incident ray.
Brewster’s Law: $\tan \theta _{B} = \frac{n_{t}}{n_{i}}$, where
θB is the Brewster’s angle
nt is the refractive index of the medium transmitted through
ni is the refractive index of the medium reflected through.
Click me for a derivation of the Brewster's equation
$$\begin{aligned} n_{i} \text{sin} \, \theta_{i} &= n_{t} \text{sin} \, \theta_{t} \\ \frac{\text{sin} \, \theta_{i}}{\text{sin} \, \theta_{t}} &= \frac{n_{t}}{n_{i}} \\ \frac{ \text{sin} \, \theta_{i}}{\text{sin} \left( 90^{\circ} \, – \theta_{i} \right)} &= \frac{n_{t}}{n_{i}} \\ \frac{\text{sin} \, \theta_{i}}{\text{cos} \, \theta_{i}} &= \frac{n_{t}}{n_{i}} \\ \text{tan} \, \theta_{i} &= \frac{n_{t}}{n_{i}} \end{aligned} $$
Explanation for polarisation by reflection:
This phenomenon can be understood qualitatively by taking into account the absorption and re-emission of light as it cross the boundary. Incident light can be resolved into parallel and perpendicular components. When incident light crosses the interface, the light is absorbed temporarily by atoms in the second medium. Electrons in these atoms oscillate back and forth in the direction of the electric field vectors in the refracted ray, perpendicular to the direction the reflected light is going.
After a brief period of time, the light is re-emitted by the atoms to form both the reflected and refracted rays. The electric field vectors in the light match the direction the electrons were oscillating and they must be perpendicular to the direction of propagation of the wave.
However, the electrons do not radiate any energy in the direction along which they oscillate. When light comes in at the Brewster’s angle, the reflected wave has no electric field vectors parallel to the plane of incidence, because the electrons oscillate in the direction of propagation of the reflected ray. Only direction possible is perpendicular to the plane of the picture, so reflected ray is linearly polarised.
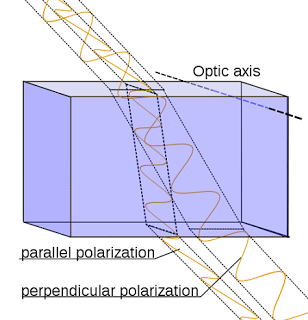
Polarization By Birefrigence
Birefringence is the division of a ray of light into two rays when they enter an optically anisotropic material.
- Optically anisotropic materials have two different indices of refraction for different direction and it’s occurance depends on the symmetry of the crystal structure.
- An example is calcite which has a refractive indices of 1.658 for one direction and 1.486 for the perpendicular direction for light with a wavelength of 589nm.
- One of the ray is ordinary ray or o-ray which propagates along the optic axis with it’s electric field perpendicular to the axis.
- The other ray is extraordinary ray or e-ray propagates perpendicular to the optic axis with it’s electric field parallel to the axis.
- Both rays travel at different velocities.