The thermal radiation is emitted over a broad spectrum of wavelengths. For a blackbody, this radiation follows the Planck radiation law:
$$P(\lambda) = \frac{2 \pi h c^{2}}{ \lambda^{5} \left( e^{\frac{hc}{\lambda k T}} – 1 \right) }$$
Pλ is power emitted per unit area per wavelength interval at wavelength λ.
– It is also called spectral emission
– SI units: W m-2 m-1 (Corresponding equal to power emitted per unit area multiplied by per wavelength interval)
Importance of this formula:
– Wien displacement law came from taking the derivative of this equation and setting to zero to find the maxima.
– Stefan-Boltzmann law came from integrating this equation over all wavelengths.
Thermal Radiation
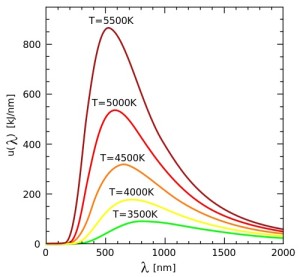
As temperature T increases:
– the thermal peak wavelength shifts proportional to T-1: Wien displacement law
– the total radiated power increases proportional to T4: Stefan-Boltzmann law
The relation between the peak wavelength and the radiant body temperature is the Wien displacement law:
$$\lambda_{peak} T = 2.898 \times 10^{-3} \, m K$$
Net Radiation Gain or Loss
The amount of electromagnetic energy absorbed by an object depends on the temperature of its surroundings. If an object at a temperature T and is fully embedded in a surrounding which is at temperature Tsurr, the rate of net energy gained (or lost) by the object due to emission and absorption of electromagnetic radiation is:
$$\frac{dQ}{dt} = \sigma A e (T^{4} – T_{surr}^{4} )$$
Hence, if T > Tsurr, the object radiates more energy than it absorbs, and its temperature decreases until equilibrium with its surroundings is reached.