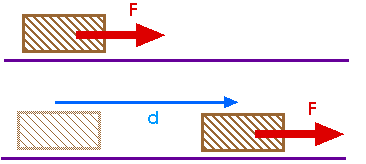
Work is done when a force moves the object in the direction of the force and is given by the product of the force and the distance moved in the direction.
- $W = F \times d$, Where W= Work, F = Constant Force (N), d = Distance moved in the direction of the force (m)
- SI Unit for work is joules (J)
- One joule is defined as the work done when a force of one newton (N) moves an object through a distance of one metre (m) in the direction of the force
- Other unit for work: Nm (Newton metre), which is obtained by multiplying the unit for force and distance.
Conditions when NO work is done
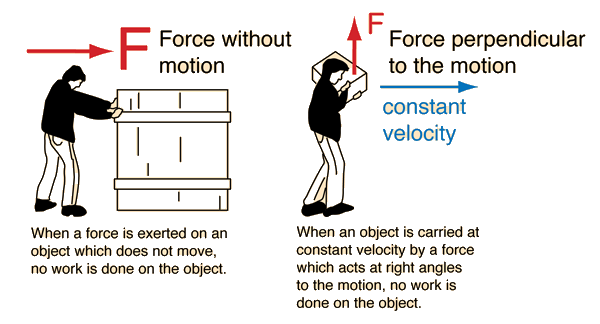
NO work is done when
- the object does not move (E.g. A boy pushing against a tree does no work)
- the direction of the force and the direction in which the point of application moves are perpendicular to one another (E.g. A boy carrying a stack of books while walking. No work is done on the stack of books in the upward direction as the stack of book is only moving horizontally.)
If no work is done for the 2 scenarios above, WHY do you feel tired (if you are the one doing the activity)?
Click to show/hide answer
For Scenario A:
When your muscles are used to exert a force on something, the individual muscle fibers are in a constant process of contracting and releasing to exert a steady force on an external object. The contracting and releasing in those muscle fibers involves force and motion, and hence, they are considered as internal work in your body. The energy shows up as warming in your muscle tissue, but if the object (tree) doesn’t move, no work is done on the object (tree).
For Scenario B:
If the box is being carried at constant velocity, then no net force is necessary to keep it in motion. The force exerted by the person is an upward force equal to the weight of the box, and that force is perpendicular to the motion. If there is no motion in the direction of the force, then no work in done by that force. However, you certainly feel like you are doing work if you carry a heavy box. The resolution of the paradox is similar to scenario A – your muscles must maintain an extra tension to stay upright under the load. This requires a greater amount of internal contraction and release of our muscle fibers, and hence internal work in our bodies. But the work done on the box is zero since by moving in a straight line at constant speed, the force (which you exert on the object) does NOT move the object in the direction of the force.
Work To Kinetic Energy
When a force moves an object, it does work on the object and the object gains kinetic energy. If there are no dissipative forces (i.e. friction/air resistance) on an object (e.g. a box), 5 joules of work done on pushing the object will translate to the object gaining 5 joules of kinetic energy.
Work to Gravitational Potential Energy
Recall that gravitational potential energy is the energy a body has due to its position above a reference level (i.e. ground). In order to find the gravitational potential energy of an object near the surface of the Earth, we need to consider the work done to lift the object of mass $m$ to a height $h$ above the reference level at constant speed.
Consider an object with mass $m$ at ground level. A force $F$ is exerted on the object in the upward direction in order to lift the object. The object is lifted at constant speed to a height of $h$ above the ground level.
Since the object is lifted at constant speed, the force $F$ is just the weight of the object. (i.e. $F = mg$) Why? If the force is larger than the weight of the object, there will be a net resultant force and the object will accelerate according to Newton’s Second Law. If the force is smaller than the weight of the object, the force will not be able to lift the object.
Since the work done by the object is given by:
$$W = F \times h$$
We will obtain:
$$\begin{aligned} W &= mg \times h \\ &= mgh \end{aligned}$$
From the above, we “derived” the equation for gravitational potential energy from work done equation!
If you are still unsure about the mechanics of the energy conversion, there are worked examples on work.
Hi! For the work done formula, could you add more about W = F x d x cosine theta, mainly the cosine theta part which I don’t really understand. Thanks!
consult books much
I’m sorry but I don’t understand the concept of how we are calcuting the velocity in the example 4. Can somebody help please?
Please refer to Energy for the relevant formulas.
In the example, it is stated that the ball of 500 g is dropped from a height of 10 m. At the height of 10m, the ball will have 50 J of gravitational potential energy, as calculated in the answer.
From the Principle of Conservation of Energy, we know that as the ball is dropping, gravitational potential energy is gradually converted into kinetic energy. This will result in the increase in the velocity of the ball as it drops.
Hence, the kinetic energy of the ball just before it hits the ground will be the gravitational potential energy at a height of 10 m. (Note: Assume that there is no losses due to air resistance) Hence, just use 50 J as the kinetic energy and use the kinetic energy formula of $E_{\text{kinetic}} = \frac{1}{2}mv^{2}$ to find the velocity.
I’m grade 7 sorry