Table of Contents
Energy
Energy of a system is defined as its capacity to do work. (Note: Work is covered in the next sub-topic)
- SI unit : joules (J)
- Scalar Quantity; Energy has magnitude only.
Principle Of Conservation Of Energy
The Principle of conservation of energy states that energy cannot be created nor destroyed in any process.
- Total amount of energy of a closed system remains constant.
- Energy can be converted/transformed from one form to another. (Note: You can think of the different forms of energy as some form of “currencies”, whereby the exchange rates among the different “currencies” are 1:1.)
- E.g. 1: A television converts electrical energy(electricity) into light, sound and thermal energies.
- E.g. 2: Burning of fuels (wood) converts stored chemical energy into heat and light energies.
- It can also be transferred from one body to another through work done and/or heat exchanges.
Forms Of Energy
- Potential Energy (Elastic, gravitational and chemical)
- Kinetic Energy (or mechanical energy)
- Electrical Energy
- Thermal Energy (or heat)
- Light
- Nuclear Energy
Kinetic Energy
Kinetic Energy, $E_{k}$ is the energy a body possessed by virtue of its motion.
- Moving objects have kinetic energy.
- Kinetic energy can be used to do work.
$$E_{k} = \frac{1}{2} m v^{2}$$
where m = Mass (in kg), v = Velocity (in $\text{m s}^{-1}$)
[A Level] Derivation Of Kinetic Energy Equation
Consider a rope attached to a box of mass m and with initial velocity $v_{i}$. The box is pulled with a constant force F by a rope and undergoes a displacement s, with a final velocity $v_{f}$
Ignoring friction and air resistance and by Conservation of Energy,
$K_{i} + W = K_{f}$, where K is Kinetic energy
$W = K_{f} \, – K_{i}$ $\rightarrow$ Equation 1
Using $v_{f}^{2} = v_{i}^{2} + 2as$
$v_{f}^{2} = v_{i}^{2} + 2 \left( \frac{F}{m} \right) s$, since $F = ma$ by Newton’s 2nd Law
$v_{f}^{2} = v_{i}^{2} + 2\left( \frac{W}{m} \right)$, since W = Fs
$mv_{f}^{2} = m v_{i}^{2} + 2W$
$W = \frac{1}{2}mv_{f}^{2} – \frac{1}{2}m v_{i}^{2}$ $\rightarrow$ Equation 2
Comparing Equation 1 and 2,
$K_{f} = \frac{1}{2} m v_{f}^{2}$ and $K_{i} = \frac{1}{2} m v_{i}^{2}$
We have:
$K = \frac{1}{2} m v^{2}$
Potential Energy
Potential Energy is the stored energy in a system.
- Example of chemical potential energy: Wood; When you burn wood, the chemical potential energy in wood is converted into thermal energy (heat) and light.
- Example of elastic potential energy: Rubber band; When you stretch a rubber band, elastic potential energy is stored in the stretched rubber band.
Gravitational Potential Energy
Gravitational Potential Energy is defined as the amount of work done in order to raise the body to the height h from a reference level.
$$G.P.E.= mgh$$
, where m = mass (in kg), g = acceleration due to gravity (in $\text{m s}^{-2}$), h = height (in m)
[A Level] Derivation Of Gravitational Potential Energy Equation
Consider a rope attached to a box of mass m and initial height of $h_{i}$. The box is lifted at a constant speed with a constant force F by a rope and undergoes a displacement $\Delta H$.
Since the box is lifted at a constant speed, the kinetic energy of the box does not change.
By Conservation of Energy,
$W = U_{f} \, – U_{i}$, where W is work done and U is gravitational potential energy
$Fd = U_{f} \, – U_{i}$
$mg \Delta H = U_{f} \, – U_{i}$
$\Delta U = mg \Delta H$
Note: W is work done by the rope
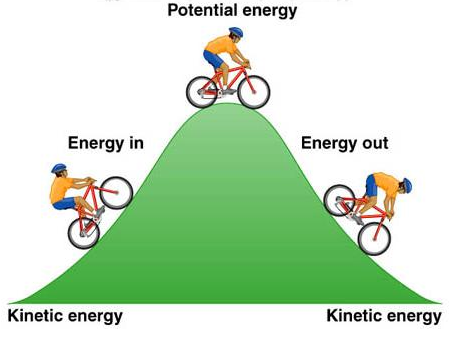
Conversion Of Gravitational Potential Energy To Kinetic Energy & Vice Versa
An object at $X$ m above the reference level (commonly taken to be the ground level) will have gravitational potential energy of $mgX$. When the object is released from the height ($X$ m), the object will have all its gravitational potential energy gradually converted into kinetic energy, just before it hits the ground. (Assuming that there is no air resistance)
From the diagram above, the conversion of kinetic energy to gravitational potential energy, and back to kinetic energy is shown.
Electrostatic Energy
Electrostatic energy is a manifestation of stored energy within charged objects. When objects acquire a net electric charge, they possess the potential for electrostatic energy. This form of energy arises due to the interactions between charged particles, such as electrons and protons. Interestingly, electrostatic energy is dynamic and can be harnessed for practical use. It is transferable through an electric current, allowing for the transmission of this energy to power various electrical devices. The understanding and control of electrostatic energy play a pivotal role in the development and functioning of electrical systems in our everyday lives.
Nuclear Energy
Nuclear energy is the potent force residing within the nucleus of an atom. This immense energy source is unleashed through nuclear reactions, specifically in processes like fission and fusion. In nuclear fission, the nucleus of an atom splits into smaller fragments, releasing a substantial amount of energy. Conversely, nuclear fusion involves the merging of atomic nuclei to create a larger nucleus, accompanied by a release of energy. Nuclear energy is not only a powerful force but also a critical component in various applications, including electricity generation in nuclear power plants. The controlled harnessing of nuclear energy has the potential to provide a significant and sustainable source of power.
Internal Energy
Internal energy, often synonymous with thermal energy, signifies the ultimate fate of diverse energy reservoirs. It embodies the total kinetic and potential energy possessed by the particles within a substance. As energy is transferred or transformed between different states, it eventually tends to become internal energy. The transfer of internal energy occurs through conduction, where heat is transferred through direct particle interaction, convection, involving the movement of heated fluids, and radiation, where energy is emitted in the form of electromagnetic waves. Internal energy is a crucial concept in understanding and manipulating heat dynamics, playing a central role in numerous natural processes and technological applications.
The next few sub-topics contain some case studies and worked examples. The case studies (oscillating pendulum and bouncing balls) and worked examples (available below) highlight the conversion of kinetic energy into gravitational potential energy and vice versa. They will help to solidify your understanding towards the concept.
Worked Examples
Example 1
A bullet with mass of 15 g has 1200 J of kinetic energy. What is its magnitude of velocity or speed?
Click here to show/hide answer
$ \begin{aligned} E_{k} &= \frac{1}{2} m v^{2} \\ 1200 &= \frac{1}{2} \times 0.015 \times v^{2} \\ v &= \sqrt{\frac{2 \times 1200}{0.015}} \\ v &= 400 \text{ m s}^{-1} \end{aligned}$
Example 2
Consider a car moving at a speed of $v \text{ ms}^{-1}$. If the speed of the car slows down to $\frac{v}{2} \text{ ms}^{-1}$, how much will the kinetic energy of the car decrease by?
Click here to show/hide answer
Recall that kinetic energy is given by $\frac{1}{2} mv^{2}$.
We will use $E_{i}$ to denote the initial kinetic energy and $E_{f}$ to denote the final kinetic energy.
We have:
$$\begin{aligned} E_{i} &= \frac{1}{2} m v^{2} \\ E_{f} &= \frac{1}{2} m \left( \frac{v}{2} \right)^{2} \end{aligned}$$
Notice that $E_{f}$ can be simplified to:
$$\begin{aligned} E_{f} &= \frac{1}{4} \frac{1}{2} m v^{2} \\ &= \frac{1}{4} E_{i}\end{aligned}$$
The kinetic energy of the car will decrease by a factor of 4.
Example 3
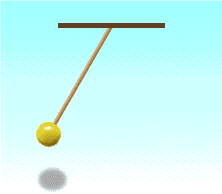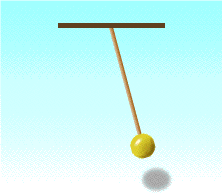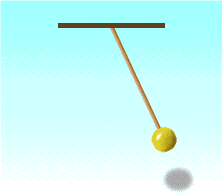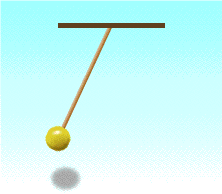
A pendulum bob swings from one end to the other. At which point (s) will the gravitational potential energy of the pendulum be (a) maximum, (b) minimum?
Click here to show/hide answer
Recall that the gravitational potential energy is given by $E_{GPE} = mgh$.
a) The gravitational potential energy of the pendulum will be the highest (maximum) when it is at the maximum height. The pendulum bob is at the maximum height at the two extreme ends of the oscillation.
b) The gravitational potential energy of the pendulum will be the lowest (minimum) when it is at the minimum height. The pendulum bob is at the minimum height at the centre of the oscillation.
Example 4
A boulder with a mass $m = 4 \, \text{kg}$ rolls off a cliff and lands on the beach below with a velocity of $v = 20 \, \text{m/s}$. Calculate:
a) The kinetic energy $E_k$ of the boulder as it lands.
b) The gravitational potential energy $\Delta E_{p}$ of the boulder when it was at the top of the cliff.
c) The height $h$ of the cliff.
Click here to show/hide answer
a) The kinetic energy $E_k$ of the boulder as it lands is calculated using the formula $E_k = \frac{1}{2} m v^2$:
$$E_k = \frac{1}{2} \times 4 \, \text{kg} \times (20 \, \text{m/s})^2 = 800 \, \text{J}$$
b) Applying the principle of conservation of energy (and neglecting energy lost in overcoming air resistance), the change in potential energy $\Delta E_p$ is equal to the kinetic energy $E_k$ of the boulder as it lands:
$$\Delta E_p = E_k = 800 \, \text{J}$$
c) If $\Delta h$ is the height of the cliff, the change in potential energy $\Delta E_p$ can be expressed as $\Delta E_p = mgh$:
$$800 \, \text{J} = 4 \, \text{kg} \times 10 \, \text{m/s}^2 \times \Delta h$$
Solving for $\Delta h$:
$$\Delta h = \frac{800 \, \text{J}}{40 \, \text{kg} \, \text{m/s}^{2}} = 20 \, \text{m}$$
Example 5: Speeding Projectile
A projectile of mass 0.02 kg travels at a speed of $1200 \text{ m s}^{-1}$. Calculate its kinetic energy.
Click here to show/hide answer
$$\begin{aligned} E_{k} &= \frac{1}{2} mv^{2} \\ &= \frac{1}{2} (0.02)(1200)^{2} \\ &= 14400 \, \text{J} \end{aligned}$$
Example 6: Lifting Object
An object with a mass of 5 kg is lifted vertically through a distance of 10 m at a constant speed. What is the gravitational potential energy gained by the object?
(Take the acceleration due to gravity to be $10 \text{ m s}^{-2}$)
Click here to show/hide answer
$$\begin{aligned} E_{gpe} &= mgh \\ &= (5)(10)(10) \\ &= 500 \, \text{J} \end{aligned}$$
Example 7: Nail In A Plank
A nail is being hammered into a plank.
- What energy does a raised hammer possess?
- When it falls, what energy will the energy in part a. convert into?
- What is the subsequent energy used for?
- Are there any other forms of energy produced? If so, name them.
Click here to show/hide answer
- Gravitational potential energy
- Kinetic energy
- It is used to drive the nail into the plank
- Some of the gravitational potential energy is converted into sound and thermal energy
Example 8: Energy Conversion Of A Stone
A boy throws a stone into the air and catches it on the way down. State the energy conversions that take place.
Note: This will be a slight variation of the Case Study 2: Bouncing Ball.
Click here to show/hide answer
- Just after the stone leaves the boy’s hand, the stone has maximum kinetic energy and minimum gravitational potential energy.
- As it rises, it’s kinetic energy is gradually converted into gravitational potential energy.
- At the point of maximum height, the stone has only gravitational potential energy. At this point, the stone has stopped momentarily so the kinetic energy of the stone is zero.
- As it is falling down, the stone’s gravitational potential energy is gradually converted into kinetic energy.
- Just before the stone reaches the boy’s hand, it will have maximum kinetic energy and minimum gravitational potential energy. However, due to energy losses from friction/air resistance, the new kinetic energy of the stone will still be smaller than it’s initial kinetic energy.
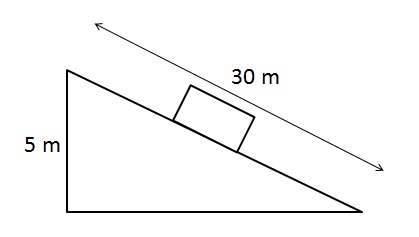
Example 9: Block On Frictionless Slope
A block of mass 5 kg slides from rest (at the top of the slope) through a distance of 30 m down a frictionless slope. What is the kinetic energy of the block at the bottom of the slope?
Click here to show/hide answer
Note that the height of the slope is 5 m. At the top of the slope, the block will possess some gravitational potential energy.
The gravitational potential energy of the block at the top of the slope is given by:
$$\begin{aligned} E_{GPE} &= mgh \\ &= 5 \times 10 \times 5 \\ &= 250 \text{ J} \end{aligned}$$
As the block slides down the slope, the gravitational potential energy will be converted into kinetic energy. Hence, when the block reaches the bottom of the slope, ALL the gravitational potential energy will be converted into kinetic energy.
The kinetic energy of the block at the bottom of the slope will be 250 J.
Example 10: Block On A Rough Slope
A block of mass 5 kg slides from rest (at the top of the slope) through a distance of 30 m down a rough slope. Considering that 30 J is dissipated as heat due to friction, what is the kinetic energy of the block at the bottom of the slope?
Click here to show/hide answer
Notice that the question is the same as the previous worked example except for the presence of friction.
Similarly, the gravitational potential energy of the block at the top of the slope will be 250 J.
As the block slides down the slope, the gravitational potential energy will be converted into kinetic energy AND heat (friction). Hence, when the block reaches the bottom of the slope, ALL the gravitational potential energy will be converted into kinetic energy AND heat (friction).
This means that:
$$\text{Gravitational Potential Energy} = \text{Kinetic Energy} + \text{Heat}$$
Given that 30 J is dissipated as heat, we have:
$$\begin{aligned} E_{kin} &= 250-30 \\ &= 220 \text{ J} \end{aligned}$$