Table of Contents
Ideal Pendulum
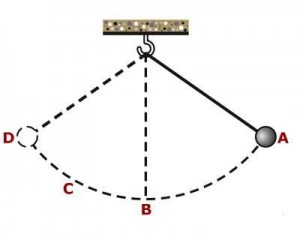
Consider an ideal pendulum (as shown in the diagram below). Note that ideal pendulum means that there is no energy lost to overcome air resistance and friction during oscillation.
When a pendulum is displaced to one side (Point A), it gains gravitational potential energy. The amount of gravitational potential energy gained will be $mgh$, where h is the height difference of point A and point B.
When the raised pendulum is released from A, it will swing towards the equilibrium position (Point B). During this movement, the gravitational potential energy is converted into kinetic energy. Hence, at B, gravitational potential energy is at minimum, while kinetic energy is at maximum.
From Point B, the pendulum will swing upwards to the other side (Point D). During this movement, the pendulum will lose kinetic energy and gain gravitational potential energy. Since this is an ideal pendulum, the pendulum will swing up to Point D, where Point D is at the same height as Point A.
Energy Conservation Equations For An Oscillating Ideal Pendulum
From the Principle of Conservation of Energy, we know that energy cannot be created nor destroyed in any process. Hence, in summary, the relevant energy conservation equations are:
From Point A to Point B,
$$\text{Initial G.P.E. of pendulum at Point A} = \text{Final K.E. of pendulum at Point B}$$
From Point B to Point D,
$$\text{Initial K.E. of pendulum at Point B} = \text{Final G.P.E. of pendulum at Point D}$$
Energy Loss Due To Resistive Forces
In the real world, resistive forces like frictional and drag forces, air resistance, convert some of the total energy of the swinging pendulum into thermal energy. This thermal energy will be dissipated into the surroundings and cannot be converted back into the kinetic or gravitational potential energy of the pendulum.
From this, it can be seen that the pendulum system will lose energy (due to air resistance) and the pendulum bob will reach a lower height with each successive swing.
However, please note that the total energy is still conserved. (Total energy referred to in this statement is the total energy of the Universe)
Energy Conversion For An Oscillating Non-Ideal Pendulum
In summary, for a non-ideal pendulum (accounting for the dissipative effects of friction and air resistance), the relevant energy conservation equations are:
From Point A to Point B,
$$\text{Initial G.P.E. of pendulum at Point A} = \text{Final K.E. of pendulum at Point B} + \text{Energy lost due to friction and air resistance}$$
From Point B to Point D,
$$\text{Initial K.E. of pendulum at Point B} = \text{Final G.P.E. of pendulum at Point D} + \text{Energy lost due to friction and air resistance}$$