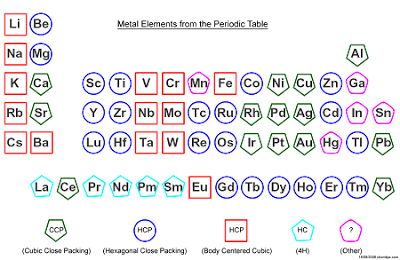
Atoms, ions or molecules in crystalline substances form a stable and orderly array known as a lattice. Crystalline solids have definite, rigid shapes with clearly defined faces. Small, 3-dimensional, repeating units called unit cells are responsible for the order found in them. The unit cell can be thought of as a box which when stacked together in 3-dimensions produces the crystal lattice.
There are a few possible arrangements of atoms in a unit cell of a crystal:
- Simple Cubic
- Body-centred Cubic (bcc)
- Face-centred Cubic (fcc)
- Hexagonal Close-packed (hcp)
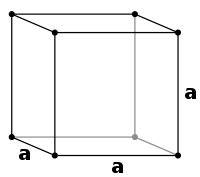
Simple Cubic
The simnple cubic unit cell is the simplest structure which consists of 8 corner atoms which form a unit cell.
Useful Information:
- Coordination number is 6. (Coordination number is the number of nearest neighbouring atoms)
- Packing efficiency = volume of spheres within unit cell/ volume of cell
$$\begin{aligned} &= \left[ \left( \frac{1}{8} \times 8 \right) \left(\frac{4}{3} \pi r^{3} \right) \right] \frac{1}{ \left(2r \right)^{3}}\\ &= \frac{\pi }{6} \\ &= 52.4 \% \end{aligned}$$
Body-centred Cubic
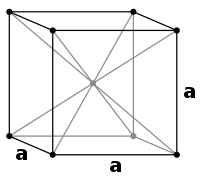
With the exception of polonium, atoms do not arrange themselves on a simple cubic pattern because they tend to pack together more closely. By examining the simple cubic arrangement, it is easy to see how it might accommodate more atoms. The most obvious empty space is that at the centre of the cube.
Many metals such as iron have a bcc structure. Certain simple binary compounds have what is essentially the bcc arrangement in which the centre of the cube is occupied by one type of atoms and the corner sites are occupied by the others.
Useful Information:
– Coordination Number is 8
– Packing Efficiency = 68%