Table of Contents
Volume
Volume (V) is defined as the amount of space occupied by a three-dimensional object as measured in cubic units.
- SI unit of volume is metres cube ($m^{3}$). It is a scalar quantity.
Density
Density ($\rho$) is defined as the mass (m) of a substance per unit volume.
- SI unit of density is kilograms per metre cube (kg m-3). It is a scalar quantity.
- Another common unit of density is $\text{g cm}^{-3}$.
- Note: $1000 \text{ kg m}^{-3} = 1 \text{ g cm}^{-3}$
Density is given by:
$$\rho = \frac{m}{V}$$
The density of a substance does not change as you move from place to place as the mass and volume does not depend on the gravitational acceleration of the point that the object is at.
- Rearranging the above equation gives: $m = V \times \rho$ and $V = \frac{m}{\rho}$. Useful if $\rho$ is known and $m$ or $V$ have to be calculated.
Densities Of Common Substances
| Solids | Density (g/cm³) |
|---|---|
| aluminium | 2.7 |
| copper | 8.9 |
| iron | 7.9 |
| gold | 19.3 |
| glass | 2.5 |
| wood (teak) | 0.80 |
| ice | 0.92 |
| Liquids | Density (g/cm³) |
|---|---|
| paraffin | 0.80 |
| petrol | 0.80 |
| pure water | 1.0 |
| mercury | 13.6 |
| Gases | Density (kg/m³) |
|---|---|
| air | 1.3 |
| hydrogen | 0.09 |
| carbon dioxide | 2.0 |
Step-By-Step Guide To Determining The Density Of A Liquid
Measuring the density of a liquid is a crucial task in various scientific, industrial, and educational settings. Density, defined as the mass per unit volume, provides valuable information about a substance’s composition and characteristics. In this article, we will explore the steps to determine the density of a liquid accurately.
Materials Needed:
- Liquid sample
- Graduated cylinder or volumetric flask
- Analytical balance
- Thermometer
- Calculator
- Density standard (optional)
Procedure:
- Select a Liquid Sample:
Begin by choosing the liquid whose density you want to measure. Ensure that the liquid is homogeneous, free from impurities, and at a temperature close to the room temperature to minimize the effects of thermal expansion. - Choose a Measuring Container:
Select an appropriate measuring container, such as a graduated cylinder or volumetric flask, based on the volume of the liquid you are working with. The container should be clean and dry. - Measure the Volume:
Pour the liquid into the graduated cylinder or volumetric flask, and carefully read the volume at the meniscus—the bottom of the concave curve formed by the liquid’s surface. Record the volume in milliliters (mL) or cubic centimeters (cm³). - Weigh the Liquid:
Use an analytical balance to weigh the liquid. Ensure that the container used to measure the liquid is empty and dry before weighing. Record the mass in grams (g). - Determine the Temperature:
Measure the temperature of the liquid using a thermometer. Temperature affects the density of a substance, and it’s crucial to account for this factor. Record the temperature in Celsius (°C). - Calculate the Density:
The formula for density $\rho$ is given by:
$\rho = \frac{m}{V}$
where $m$ is the mass and $V$ is the volume. Use the recorded mass and volume values to calculate the density. - Compare with a Standard:
If possible, compare your calculated density with a known density standard for the liquid to verify the accuracy of your measurements. - Repeat for Accuracy:
To ensure precision and reliability, repeat the experiment multiple times, especially if the liquid’s composition is variable.
Determining the density of a liquid involves a systematic approach combining careful measurements and calculations. Following these steps will help you obtain accurate and reliable results, making this process essential in various scientific, educational, and industrial applications.
Step-By-Step Guide To Determining The Density Of A Solid
Measuring the density of solids is a fundamental process in various scientific, industrial, and academic fields. The density of a solid, defined as its mass per unit volume, provides crucial insights into its composition and properties. In this article, we will delve into the steps involved in determining the density of solids accurately.
Materials Needed:
- Solid sample
- Electronic balance or analytical balance
- Ruler or calipers
- Graduated cylinder or water displacement apparatus
- Calculator
- Density standard (optional)
Procedure:
- Choose a Solid Sample:
Begin by selecting the solid whose density you want to determine. Ensure that the sample is homogeneous and free from any irregularities or voids. - Measure the Dimensions:
Use a ruler or calipers to measure the dimensions of the solid. For regular-shaped solids like cubes or cylinders, measure the length, width, and height. For irregular shapes, record the necessary dimensions to calculate the volume. - Calculate the Volume:
Depending on the shape of the solid, use the appropriate formula to calculate its volume. For a cube or rectangular prism, the volume $V$ is given by:
$$V = \text{length} \times \text{width} \times \text{height}$$
For irregular shapes, use the appropriate geometry formula or consider water displacement. - Weigh the Solid:
Use an electronic or analytical balance to measure the mass of the solid. Ensure that the balance is calibrated, and the solid is dry and free from any contaminants. - Calculate the Density:
Apply the formula for density $\rho$:
$\rho = \frac{m}{V}$
where $m$ is the mass and $V$ is the volume. Utilize the recorded mass and volume values to calculate the density. - Compare with a Standard:
If available, compare the calculated density with a known density standard for the solid. This step helps validate the accuracy of your measurements. - Repeat for Accuracy:
To enhance precision, repeat the experiment multiple times, especially if the solid’s composition or structure is variable.
Measuring the density of solids involves meticulous attention to detail, combining accurate measurements and calculations. By following these steps, you can ensure that your density determination is reliable and valuable for understanding the properties of different solid materials in scientific, industrial, and educational contexts.
Worked Examples
Example 1
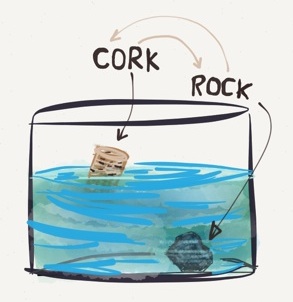
Examine the figure above. Why does the cork float and the rock sink in water?
Show/Hide Answer
The density of a substance determines whether it will float or sink in different liquids (or gases).
The cork is less dense than water $\rightarrow$ it floats in water.
The rock is denser than water $\rightarrow$ it sinks in water.
Example 2
A block of concrete with dimensions 0.4 m, 0.3 m and 0.1 m has a density of $2500 \text{ kg m}^{-3}$. Calculate the mass of the block.
Show/Hide Answer
$$\begin{aligned} V &= 0.4 \times 0.3 \times 0.1 \\ &= 0.012 \text{ m}^{3} \end{aligned}$$
From the density equation ($\rho = \frac{m}{V}$), we have:
$$\begin{aligned} m &= \rho V \\ &= 2500 \times 0.012 \\ &= 30 \text{ kg} \end{aligned}$$
Example 3
Taking the density of copper as 9 g/cm³, determine:
a) the mass of 5 cm³
b) the volume of 63 g.
Show/Hide Answer
a) Let the density be denoted as $\rho = 9 \, \text{g/cm}^3$, the volume as $V = 5 \, \text{cm}^3$, and the mass as $m$.
The mass $m$ can be calculated using $m = V \times \rho$, which yields:
$$\begin{aligned} m &= 5 \, \text{cm}^3 \times 9 \, \text{g/cm}^3 \\ &= 45 \, \text{g} \end{aligned}$$
b) For this part, let the density be $\rho = 9 \, \text{g/cm}^3$, the mass be $m = 63 \, \text{g}$, and the volume be denoted as $V$. Solving for $V$ using $V = \frac{m}{\rho}$, we get:
$$\begin{aligned} V &= \frac{63 \, \text{g}}{9 \, \text{g/cm}^3} \\ &= 7 \, \text{cm}^3 \end{aligned}$$
Example 4
An aluminum sheet weighs 200 g and has a volume of 73 cm³. Determine the density of aluminum.
Show/Hide Answer
Let the mass be denoted as $m = 200 \, \text{g}$ and the volume as $V = 73 \, \text{cm}^3$. The density $\rho$ can be calculated using the formula $\rho = \frac{m}{V}$. Substituting the given values, we get:
$$\rho = \frac{200 \, \text{g}}{73 \, \text{cm}^3} \approx 2.74 \, \text{g/cm}^3$$
Example 5
Given the density of lead as $11 \, \text{g/cm}^3$, determine:
a) the mass of 4 cm³
b) the volume of 55 g.
Show/Hide Answer
a) Let the volume be $V = 4 \, \text{cm}^3$. The mass $m$ can be calculated using $m = \rho \times V$, where $\rho = 11 \, \text{g/cm}^3$.
$$\begin{aligned} m &= 11 \, \text{g/cm}^3 \times 4 \, \text{cm}^3 \\ &= 44 \, \text{g} \end{aligned}$$
b) Let the mass be $m = 55 \, \text{g}$. The volume $V$ can be calculated using $V = \frac{m}{\rho}$.
$$\begin{aligned} V &= \frac{55 \, \text{g}}{11 \, \text{g/cm}^3} \\ &= 5 \, \text{cm}^3 \end{aligned}$$