In an adiabatic process, there is no heat exchange between the system and its surroundings (Q = 0). For such a process, the first law gives ΔE = W.
This means that the internal energy increases if work is done on the system, and this usually leads to a temperature rise. If work is done by the system, the internal energy decreases, which is usually accompanied by a temperature drop.
Examples of adiabatic processes:
– Reactions or transformations taking place in a thermal-insulated chamber.
– Fast processes for which there is not enough time for heat exchange to take place.
- E.g. Operating a spray can, bicycle pump or opening a carbonated beverage can.
- Air masses ascending or descending in the Earth’s atmosphere.
Derivation of the PV relation for an adiabat of an ideal gas.
$$\begin{aligned} dE &= \delta Q + \delta W \\ &= 0 \, – P \, dV \end{aligned}$$
Since dE = nCvdT, we have
$$n C_{v} \, dT = \, – P \, dV$$
This means that as the gas is compressed adiabatically (dV < 0), its temperature rises (dT > 0), which is thus called adiabatic heating.
Conversely, if the gas is expanded adiabatically, its temperature falls, i.e., adiabatic cooling.
We now need to eliminated dT to find the relationship between P and V during the transformation.
By differentiating the ideal gas equation PV = nRT, we get:
$$V \, dP + P \, dV = nR \, dT$$
By substituting the adiabatic relation (Equation 1) into the right hand side of the equation above, we get:
$$V \, dP + P \, dV = \, – nR \frac{P \, dV}{n C_{v}}$$
Rearranging,
$$\begin{aligned} V \, dP + \left( 1 + \frac{R}{C_{v}} \right) P \, dV \, &= 0 \\ V \, dP + \left( \frac{C_{p}}{C_{v}} \right) P \, dV \, &= 0 \\ V \, dP + \gamma P \, dV \, &= 0 \end{aligned}$$
Integrating both sides of the equation, we obtain:
$$\int\limits_{P_{1}}^{P_{2}} \frac{1}{P} \, dP + \gamma \int\limits_{V_{1}}^{V_{2}} \frac{1}{V} \, dV = 0$$
Hence,
$$P_{1} V_{1}^{\gamma} = P_{2} V_{2}^{\gamma}$$
Substitute in the ideal gas law and you get the other forms,
$$\begin{aligned}T_{1} V_{1}^{\gamma \, – 1} \, &= T_{2} V_{2}^{\gamma \, -1} \\ T_{1}^{\gamma} P_{1}^{1 \, – \gamma} \, &= T_{2}^{\gamma}P_{2}^{1 \, – \gamma} \end{aligned}$$
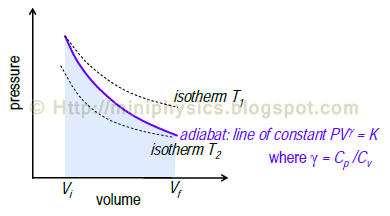
Adiabatic ideal gas process
Equation of the adiabat (line of constant $PV^{\gamma}$)
$$P_{1} V_{1}^{\gamma} = P_{2} V_{2}^{\gamma} = K$$
Adiabatic work done by the gas,
$$ \begin{aligned} W_{out} &= \int\limits_{V_{i}}^{V_{f}} P \, dV \\ &= \int\limits_{V_{i}}^{V_{f}} \frac{K}{V^{\gamma}} \, dV \\ &= K \frac{ \left( V_{f}^{1 \, – \gamma} \, – V_{i}^{1 \, – \gamma} \right)}{1 \, – \gamma} \end{aligned}$$