Ampere’s Law can be used to simplify problems with a certain symmetry.
Example: Magnetic Field Inside A Long Cylindrical Conductor
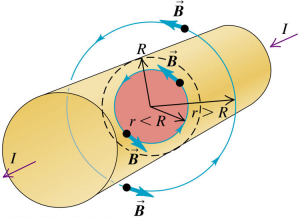
A cylindrical conductor with radius R carries a current I. The current is uniformly distributed over the cross-sectional area of the conductor. Find the magnetic field as a function of the distance r from the conductor axis for points both inside ($r < R$) and outside ($r > R$) the conductor.
From Ampere’s Law, we have:
$$\oint \vec{B}.d\vec{l} = \mu_{0} I _{encl}$$
We will take the ampere loop to be a circle. Hence, for points inside the conductor, the ampere loop will be a circle with radius r, where $r < R$. The current enclosed will be $\frac{I}{\pi R^{2}} \times \pi r^{2}$.
$$\begin{aligned} B \times 2 \pi r &= \mu_{0} \frac{I}{\pi R^{2}} \times \pi r^{2} \\ B &= \frac{\mu_{0}I}{2 \pi} \frac{r}{R^{2}} \end{aligned}$$
For points outside the conductor, the ampere loop will be a circle of radius r, where $r > R$. The current enclosed will just be I.
$$\begin{aligned} B \times 2 \pi r &= \mu_{0} I \\ B &= \frac{\mu_{0} I}{2 \pi r} \end{aligned}$$
Example: Magnetic Field Of A Solenoid
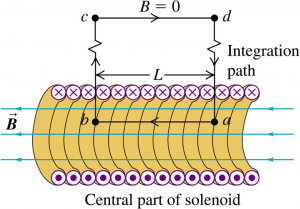
A solenoid consists of a helical winding of wire on a cylinder, usually circular in cross section. If the solenoid is long in comparison with its cross-sectional diameter and the coils are tightly wound, the internal field near the midpoint of the solenoid’s length is very nearly uniform over the cross section and parallel to the axis, and the external field near the midpoint is very small. Use Ampere’s law to find the field at or near the center of such a long solenoid. The solenoid has n turns of wire per unit length and carries a current I.
From Ampere’s Law, we have:
$$\oint \vec{B}.d\vec{l} = \mu_{0} I _{encl}$$
Following the integration path, we have:
$$\begin{aligned} \oint \vec{B}.d\vec{l} &= \mu_{0}nLI \\ \int\limits_{a}^{b} \vec{B}.d\vec{l} + \int\limits_{b}^{c} \vec{B}.d\vec{l} + \int\limits_{c}^{d} \vec{B}.d\vec{l} + \int\limits_{d}^{a} \vec{B}.d\vec{l} &= \mu_{0}nLI \\ BL + 0 + 0 + 0 &= \mu_{0}nLI \\ B &= \mu_{0}nI \end{aligned}$$
Example: Magnetic Field Of A Toroidal Solenoid
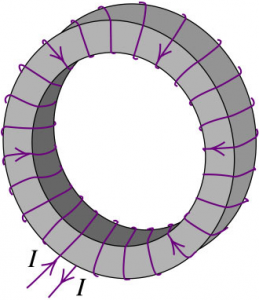
The figure above shows a doughnut-shaped toroidal solenoid, wound with N turns of wire carrying a current I. Find the magnetic field at all points.
From Ampere’s Law, we have:
$$\oint \vec{B}.d\vec{l} = \mu_{0} I _{encl}$$
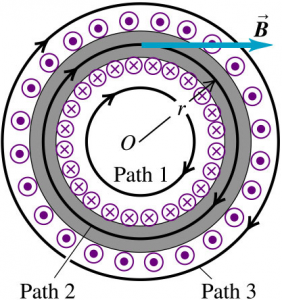
Let’s consider path 1,
No current is enclosed by the path. Hence, the magnetic field along the path is 0.
Let’s consider path 3,
The net current enclosed by the path is 0. Hence, the magnetic field along the path is 0.
Let’s consider path 2,
$$\begin{aligned} B \times 2 \pi r &= \mu_{0} NI \\ B &= \frac{\mu_{0} NI}{2 \pi r} \end{aligned}$$
Next: Electromagnetic Induction Experiments
Back To Electromagnetism (UY1)