Derivation Of Moment Of Inertia Of A Hollow/Solid Cylinder

Step-By-Step Guide For Derivation Of The Moment Of Inertia Of A Hollow/Solid Cylinder

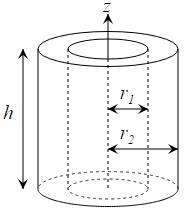
A hollow cylinder has an inner radius $R_1$, mass $M$, outer radius $R_2$ and length $L$. Calculate/derive its moment of inertia about its central axis.

Moment Of Inertia Of A Hollow/Solid Cylinder is:

$$I = \frac{1}{2}M(R_{2}^{2}+R_{1}^{2})$$

Moment Of Inertia For Hoop Or Thin Cylindrical Shell is:

$$I = M R^{2}$$

Moment Of Inertia For Disk Or Solid Cylinder is:

$$I = \frac{1}{2} M R^{2}$$

Outline Of Solution

This kind of solution might be your initial encounter with this concept, so we will walk through it together with clear steps and explanations.

Step 1: Conceptualizing the Problem

Understanding the Cylinder: Imagine the cylinder as an object with a mass distributed between its inner and outer surfaces. Unlike a solid cylinder, the mass of a hollow cylinder is distributed across the volume between $R_1$ and $R_2$, with uniform density throughout this volume.
Axis of Rotation: The axis around which we calculate the moment of inertia runs centrally along the cylinder’s length, equidistant from its curved surface.

Step 2: Dividing the Cylinder into Elements

Slicing the Cylinder: Visualize slicing the cylinder into an infinite number of thin concentric rings. Each ring represents a differential element with a tiny thickness $dr$, maintaining the cylinder’s length $L$.
Mass of a Ring: Each differential ring has a small mass $dm$. This mass is part of the cylinder’s total mass $M$, distributed across the volume defined by the outer and inner radii.
Position Variable: A variable $r$, representing the radius from the central axis to any point within the thickness of a ring, will be used to calculate the moment of inertia of each differential element.

Step 3: Mathematical Formulation

Expression for $dm$: The mass distribution across the cylinder’s volume allows us to express $dm$ as $dm = \rho \: dV$, correlating the mass of a differential ring to its volume.
Moment of Inertia of a Ring: The moment of inertia $dI$ for a differential ring at a radius $r$ is given by $dI = dm \cdot r^2$, encapsulating each ring’s contribution to the cylinder’s total moment of inertia.

Step 4: Integrating Over the Cylinder

Setting Up the Integral: To find the total moment of inertia $I$, integrate $dI$ from $R_1$ to $R_2$. This accounts for the entire volume of the hollow cylinder.
Integration Process: The integration will extend across all radii from $R_1$ to $R_2$, incorporating each differential ring’s contribution to the total moment of inertia.

Step 5: Final Calculation

Computing $I$: Integrating the expression for $dI$ within the specified limits yields the formula for the moment of inertia of the hollow cylinder about its central axis.

Conclusion: By dissecting the hollow cylinder into infinitesimally thin rings, calculating the moment of inertia for each, and integrating these across the cylinder’s radius, we derive the total moment of inertia around the central axis. This approach marries physics concepts with calculus techniques to address the problem effectively.

Full Derivation Of Moment Of Inertia Of A Hollow/Solid Cylinder

We begin our derivation of the moment of inertia equation with:

$$dI = r^{2} \: dm$$

Now, we have to find dm.

To calculate $dm$, which represents the mass of an infinitesimally thin ring, we introduce the concept of density ($\rho$) multiplied by the volume ($dV$) of the ring:

$$dm = \rho \: dV$$

We’ve introduced dV in the above equation, so, we have to find out what dV is. We define $dV$ as the product of the cross-sectional area ($dA$) of the ring and its length ($L$):

$$dV = dA \: L$$

The differential area ($dA$) can be understood as the difference in area between a ring of radius $r + dr$ and one of radius $r$, giving us:

$$dA = \pi (r + dr)^{2}-\pi r^{2}$$

$$dA = \pi (r^{2} + 2rdr + (dr)^{2})-\pi r^{2}$$

Simplifying, and noting that the term $(dr)^2$ is negligible (since the square of an infinitesimally small number is effectively zero), we arrive at:

$$dA = 2 \pi r \: dr$$

Note: An alternative approach to find $dA$ involves direct differentiation of the area formula for a circle, $A = \pi r^2$, with respect to $r$, yielding:
$$dA = 2 \pi r \: dr$$

Substituting $dA$ into the expression for $dV$, we get

$$dV = 2 \pi r L \: dr$$

Using the above equation, substitute into dm, we get

$$dm = 2 \rho \pi r L \: dr$$

Finally, we have an expression for dm. We substitute that into the dI equation,

$$dI = 2 \rho \pi r^{3} L \: dr$$

To find the total moment of inertia $I$, we integrate $dI$ from the inner radius $R_1$ to the outer radius $R_2$:

$$I = 2 \rho \pi L \: \int\limits_{R_{1}}^{R_{2}} r^{3} \: dr$$

Integrating:

$$\begin{aligned} I &= 2 \rho \pi L \int\limits_{R_{1}}^{R_{2}} r^{3} dr \\ &= 2 \rho \pi L \left[ \frac{1}{4}r^4 \right]_{R{1}}^{R_{2}} \\ &= 2 \rho \pi L \left( \frac{1}{4}R_{2}^4-\frac{1}{4}R_{1}^4 \right) \\ &= \frac{1}{2} \rho \pi L \left( R_{2}^4-R_{1}^4 \right) \end{aligned}$$

Now, the density $\rho$ can be expressed as the mass of the cylinder ($M$) divided by its volume, which for a hollow cylinder is $\pi (R_{2}^{2}-R_{1}^{2}) L$. Thus, $\rho$ is:

$$\rho = \frac{M}{\pi (R_{2}^{2}-R_{1}^{2}) L}$$

Substituting this back into the integrated solution, we have:

$$I = \frac{1}{2}M(R_{2}^{2}+R_{1}^{2})$$

We’re done!

Special Cases: Moment Of Inertia For Thin Cylindrical Shell & Solid Cylinder

The moment of inertia ($I$) for rotating bodies significantly depends on the distribution of mass relative to the axis of rotation. Two noteworthy cases in cylindrical geometry are the thin cylindrical shell (or hoop) and the solid cylinder (or disk). The formulas for these cases are derived from the general equation for a hollow cylinder by setting specific values for the inner ($R_1$) and outer ($R_2$) radii.

Moment Of Inertia For Hoop Or Thin Cylindrical Shell

In the case of a hoop or a thin cylindrical shell, the thickness is negligible compared to its radius, effectively making $R_1 = R_2 = R$. This simplification leads to the moment of inertia formula:

$$I = M R^{2}$$

This scenario assumes all the mass is concentrated at a single distance $R$ from the axis of rotation, leading to the maximum moment of inertia for a given mass and radius. The hoop or thin cylindrical shell illustrates how the moment of inertia increases as mass is distributed further from the axis of rotation.

Moment Of Inertia For Disk Or Solid Cylinder

For a disk or a solid cylinder, the entire volume is filled with mass, meaning the inner radius is $R_1 = 0$, and only the outer radius ($R$) defines the shape:

$$I = \frac{1}{2} M R^{2}$$

This formula reflects the distribution of mass from the axis of rotation to the outer edge, averaging the contribution of each mass element, thus resulting in a smaller moment of inertia compared to a thin shell for the same mass and outer radius.

Sanity Check

The expectation that the moment of inertia ($I$) should be highest for a hoop or cylindrical shell is intuitive when considering the distribution of mass. For the hoop, all the mass is at the maximum distance from the axis, maximizing $r^2$ in the $I = M R^{2}$ formula. In contrast, the disk or solid cylinder distributes mass closer to the axis on average, leading to a lower moment of inertia ($I = \frac{1}{2} M R^{2}$). This aligns with the physical principle that objects with mass distributed further from their rotation axis require more torque to achieve the same angular acceleration, indicating a higher moment of inertia.