Derivation Of Moment Of Inertia Of An Uniform Solid Sphere

Step-By-Step Guide For Derivation Of Moment Of Inertia Of An Uniform Solid Sphere

An uniform solid sphere has a radius R and mass M. calculate its moment of inertia about any axis through its centre.

Moment Of Inertia Of An Uniform Solid Sphere is:

$$I = \frac{2}{5} M R^{2}$$

Outline Of Solution

This kind of solution might be your initial encounter with this concept, so we will walk through it together with clear steps and explanations.

Step 1: Conceptualizing the Problem

Understanding the Sphere: View the sphere as a three-dimensional object with uniform mass distribution, meaning each volume element of the sphere has the same density.
Axis of Rotation: The axis around which we are calculating the moment of inertia passes through the center of the sphere, allowing us to use symmetry in our calculations.

Step 2: Dividing the Sphere into Elements

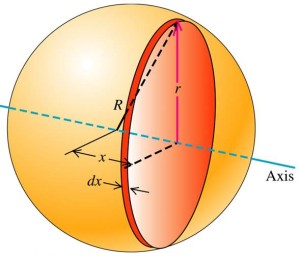
Slicing the Sphere: Imagine dividing the sphere into an infinite number of thin cylindrical slices. This approach helps us account for the mass and position of each segment when calculating the total moment of inertia.
Mass of a Slice: Each cylindrical slice can be considered to have a mass $dm$, representing a small portion of the sphere’s total mass $M$, related to a thin slice volume $dV$.
Position Variable: We’ll use the radius $r$ of each cylindrical slice as the variable representing the distance from the center to any point within the slice, crucial for our moment of inertia calculation.

Step 3: Mathematical Formulation

Expression for $dm$: Given the sphere’s uniform density, the mass of a slice is related to its volume by $dm = \rho \: dV$, where $\rho$ is the density of the sphere.
Moment of Inertia of a Slice: The moment of inertia $dI$ for a thin cylindrical slice at a radius $r$ is given by $dI = \frac{1}{2}r^2 \: dm$. This formula captures each slice’s contribution to the sphere’s total moment of inertia.

Step 4: Integrating Over the Sphere

Setting Up the Integral: To find the sphere’s total moment of inertia $I$, integrate $dI$ over the entire volume of the sphere. The integration takes into account the spherical symmetry and the distribution of mass.
Integration Process: The integration is performed by considering all cylindrical slices from the center of the sphere to its outer surface, incorporating the sphere’s radius $R$.

Step 5: Final Calculation

Computing $I$: The final step involves integrating the expression for $dI$ over the sphere’s volume. This will provide the formula for the moment of inertia of the sphere about an axis through its center.

Conclusion

By dividing the sphere into infinitesimally small cylindrical slices, calculating the moment of inertia for each, and integrating these contributions across the sphere, we derive the total moment of inertia for the sphere about its center. This approach blends physics principles with calculus techniques to address the problem effectively.

Full Derivation Of Moment Of Inertia Of An Uniform Solid Sphere

To calculate the moment of inertia ($I$) of a uniform solid sphere, let’s start by recalling the formula for the moment of inertia of a solid cylinder about its central axis:

Main Article: Derivation Of Moment Of Inertia Of A Hollow/Solid Cylinder

$$I = \frac{1}{2} M R^{2}$$

Given this, for a differential element of the sphere, the differential moment of inertia ($dI$) can be expressed as:

$$dI = \frac{1}{2} r^{2} \: dm$$

,where $r$ is the radius of the differential cylindrical slice, and $dm$ is its mass.

To find $dm$, we first express it in terms of the density ($\rho$) and the differential volume ($dV$):

$$dm = \rho \: dV$$

For a thin cylindrical slice of the sphere, $dV$ can be represented as the product of the cross-sectional area ($\pi r^{2}$) and the thickness ($dx$):

$$dV = \pi r^{2} \: dx$$

Substituting the expression for $dV$ into $dm$ gives:

$$dm = \rho \pi r^{2} \: dx$$

Then, substituting $dm$ into $dI$ yields:

$$dI = \frac{1}{2} \rho \pi r^{4} \: dx$$

To relate the radius of the cylindrical slice ($r$) with the sphere’s radius ($R$) and the position $x$ along the axis through the center, we use Pythagoras’ theorem. Hint: Notice that $x$, $r$ and $R$ makes a triangle above.

$$r^{2} = R^{2}-x^{2}$$

Substituting $r^{2}$ in the $dI$ expression:

$$dI = \frac{1}{2} \rho \pi (R^{2}-x^{2})^{2} \: dx$$

Integrating $dI$ from $-R$ to $R$ to cover the entire sphere:

$$I = \frac{1}{2} \rho \pi \int\limits_{-R}^{R} (R^{2}-x^{2})^{2} \: dx$$

Solving The Integral

Expanding the integrand,

$$(R^{2}-x^{2})^{2} = R^{4}-2R^{2}x^{2} + x^{4}$$

Thus, the integral becomes

$$I = \frac{1}{2} \rho \pi \int_{-R}^{R} (R^{4}-2R^{2}x^{2} + x^{4}) \, dx$$

We can integrate each term in the expression directly:

$$I = \frac{1}{2} \rho \pi \left( R^{4}x-\frac{2R^{2}x^{3}}{3} + \frac{x^{5}}{5} \right) \Big|_{-R}^{R}$$

Let’s evaluate this at the limits from $-R$ to $R$:

For $x = R$:

$$R^{4}R-\frac{2R^{2}R^{3}}{3} + \frac{R^{5}}{5} = R^{5}-\frac{2R^{5}}{3} + \frac{R^{5}}{5}$$

For $x = -R$ (noting that $x^{3}$ and $x^{5}$ will change signs for odd powers, but the even powers remain positive):

$$-R^{5} + \frac{2R^{5}}{3}-\frac{R^{5}}{5}$$

Adding these, since the integral calculates the difference, effectively doubling the result because the function is symmetric about $x=0$:

$$\begin{aligned} 2\left(R^{5}-\frac{2R^{5}}{3} + \frac{R^{5}}{5}\right) &= 2R^{5}\left(1-\frac{2}{3} + \frac{1}{5}\right) \\ &= 2R^{5}\left(\frac{15}{15}-\frac{10}{15} + \frac{3}{15}\right) \\ &= 2R^{5}\left(\frac{8}{15}\right) \end{aligned}$$

Substituting this result back into the expression for $I$:

$$I = \frac{1}{2} \rho \pi \left(2R^{5}\left(\frac{8}{15}\right)\right)$$

$$I = \frac{8}{15} \rho \pi R^{5}$$

Now, to find the density ($\rho$) of the sphere, we use its mass ($M$) and volume ($V$):

$$\rho = \frac{M}{V}$$

$$\rho = \frac{M}{\frac{4}{3} \pi R^{3}}$$

Finally, substituting $\rho$ into the formula for $I$: