The moment of inertia is a measure of the resistance of an object to changes in its rotational motion, just as mass is a measure of the tendency of an object to resist changes in its linear motion.
Mass is an intrinsic property of an object, but I depends on the physical arrangement of that mass and the axis of rotation.
Dimension: ML2; units kg.m2.
Since the moment of inertia, I, is defined as
$$I = \sum\limits_{i} m_{i}r_{i}^{2}$$
hence, the kinetic energy can be written as
$$K_{R} = \frac{1}{2} I \omega^{2}$$
The moment of inertia for an extended rigid object (divided into small elements) can be written as:
$$\begin{aligned} I \, &= \lim_{\Delta m_{i} \rightarrow 0}{\sum\limits_{i} \Delta m_{i} r_{i}^{2}} \\ &= \int r^{2} \, dm \\ &= \int pr^{2} \, dV \end{aligned}$$
Derivation Of Moment Of Inertia Of Common Shapes:
- Summary
- Uniform Rigid Rod (“Beginners’ Lesson”)
- Hollow/solid Cylinder
- Uniform Solid Sphere
- Thin Spherical Shell
Parallel Axis Theorem
Parallel axis theorem states that the moment of inertia about any axis parallel to and at distance D away from the axis that passes through the centre of mass is:
$$I = I_{\text{CM}} + MD^{2}$$
This theorem works for any solids and shapes.
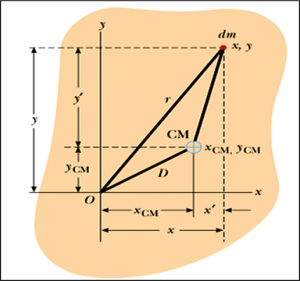
Proof Of Parallel Axis Theorem
Consider the shape above,
We notice that:
$$\begin{aligned} x &= x^{\prime} + x_{\text{CM}} \\ y &= y^{\prime} + y_{\text{CM}} \end{aligned}$$
From the moment of inertia equation:
$$\begin{aligned} I &= \int r^{2} \, dm \\ &= \int \left( x^{2} + y^{2} \right) \, dm \\ &= \int \left[ \left( x^{\prime}+ x_{\text{CM}} \right)^{2} + \left( y^{\prime} + y_{\text{CM}} \right)^{2} \right] \, dm \\ &= \int \left[ x^{\prime} + y^{\prime} \right] \, dm + \int \left[ x_{\text{CM}}^{2} + y_{\text{CM}}^{2} \right] \, dm + 2x_{\text{CM}} \int x^{\prime} \, dm + 2 y_{\text{CM}} \int y^{\prime} \, dm \end{aligned}$$
Since in the centre of mass frame, we have:
$$\begin{aligned} \int x^{\prime} \, dm &= x_{\text{CM}}^{\prime} = 0 \\ \int y^{\prime} \, dm &= y_{\text{CM}}^{\prime} = 0 \end{aligned}$$
Due to the null results above, we obtain:
$$\begin{aligned} I &= \int r^{\prime 2} \, dm + D^{2} \int \, dm \\ I &= I_{\text{CM}} + MD^{2} \end{aligned}$$
Done.
Perpendicular Axis Theorem
The perpendicular axis theorem states that the sum of moments of inertia about any two perpendicular axes in the plane of the body is equal to the moment of inertia about an axis through the point of intersection perpendicular to the plane of the object.
$$I_{z} = I_{x} + I_{y}$$
This theorem only works for plane figures (2-D bodies: bodies of negligible thickness).
Radius Of Gyration
It is often useful to define radius of gyration, $k$, as:
$$\begin{aligned} I &= Mk^{2} \\ k &= \sqrt{\frac{I}{M}} \end{aligned}$$
Radius of gyration functions as some sort of “average” radius – as if all the mass of the object were concentrated in this distance from the axis.
For example:
The radius of gyration for a uniform cylinder and sphere is:
$$\begin{aligned} k_{\text{cylinder}} &= R \sqrt{\frac{1}{2}} = 0.707 R \\ k_{\text{sphere}} &= R \sqrt{\frac{2}{5}} = 0.632 R \end{aligned}$$
Next: Torque & Angular Acceleration