Torque
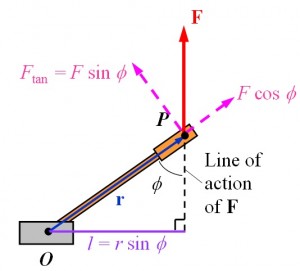
Consider a force $\vec{F}$ acting on a rigid body at point $P$ in the direction as shown. The rod is pivoted so that it can only rotate about point $O$.
In this case, the torque $\tau$ of force $\vec{F}$ about $O$ is defined as:
$$\begin{aligned} \tau &= Fl \\ &= rF \sin{\theta} \\ &= F_{\text{tan}}r \end{aligned}$$
,where $l$ is the moment arm (lever arm) of the force, the shortest distance from $O$ to the line of action of the force $\vec{F}$.
Only the component perpendicular to $\vec{r}$, $F\sin{\theta}$, of the force $\vec{F}$ causes rotation.
The component along $\vec{r}$, $F \cos{\theta}$, has no effect on the rotation of the rigid body
Torque Is A Vector
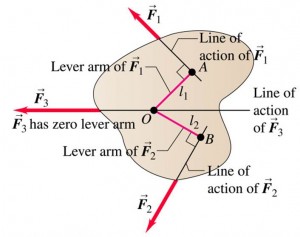
If two or more forces are acting on a rigid object, it is assumed that the sign of a torque is positive if the turning tendency of the force is counter-clockwise and is negative if the turning tendency is clockwise.
$$\begin{aligned} \sum \tau &= \tau_{1} + \tau_{2} + \tau_{3} \\ &= F_{1}l_{1}-F_{2}l_{2} + 0 \end{aligned}$$
Difference Between Torque And Force
Forces can cause a change in linear motion.
Forces can also cause a change in rotational motion, but the effectiveness of these forces in causing the change depends on both the forces and the moment of forces – torque.
The dimension of torque is force times length.
SI unit is Nm.
Torque & Angular Acceleration
Consider a particle with mass $m$ rotating in a circle of radius $r$ under the influence of a tangential force $F_{t}$ and a radial force $F_{r}$.
Let’s try to link torque with angular acceleration, $\alpha$.
$$\begin{aligned} \tau &= rF_{t} \\ &= r \left( m a_{t} \right) \\ &= r \left( mr \alpha \right) \\ &= \left( mr^{2} \right) \alpha \end{aligned}$$
Notice that $mr^{2}$ is just the moment of inertia of the particle. Hence,
$$\tau = I \alpha$$
Hence, the torque acting on a particle is proportional to its angular acceleration.
Now, the above relationship is derived with a single particle in mind. What about an extended object?
For an extended object, each mass element $dm$ rotates about the origin (z-axis).
$$\begin{aligned} d \tau &= r \, dF_{t} \\ &= r \left( dm \right) a_{t} \\ &= \left( r^{2} \, dm \right) \alpha \end{aligned}$$
Integrating over all mass elements:
$$\begin{aligned} \tau &= \int \left( r^{2} \, dm \right) \alpha \\ &= \alpha \int r^{2} \, dm \\ \tau &= I \alpha \end{aligned}$$
We obtain the same relationship between torque and angular acceleration for extended object.