For a rolling object, the axis of rotation is not fixed in space. The axis of rotation travels with the rolling object.
There are several assumptions to simplify the analysis of rolling objects:
- Homogeneous rigid body
- High degree of symmetry (E.g. Cylinder, sphere, hoop)
- Pure rolling motion (rolling without slipping)
- Rolling motion along a flat surface (inclined, horizontal or even vertical)
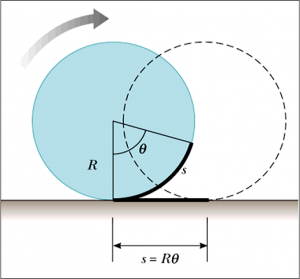
When the cylinder rotates through an angle $\theta$, its centre of mass moves a linear distance $s$.
We know from elementary mathematics that the arc length, s, is given by $s = R \theta$. Using this we can calculate the velocity of the centre of mass.
$$\begin{aligned} v_{\text{CM}} &= \frac{ds}{dt} \\ &= R \frac{d \theta}{dt} \\ &= R \omega \end{aligned}$$
Using $v_{\text{CM}}$, the acceleration of the centre of mass:
$$\begin{aligned} a_{\text{CM}} &= \frac{dv_{\text{CM}}}{dt} \\ &= R \frac{d \omega}{dt} \\ &= R \alpha \end{aligned}$$
Done.
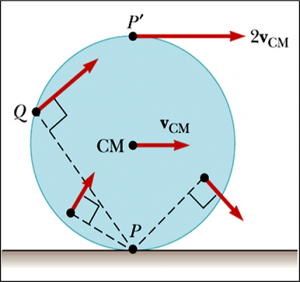
The figure above shows a rolling cylinder. All points on the cylinder have the same angular speed, but different linear velocity.
The linear velocity of any point is in a direction perpendicular to the line from that point to the contact point $P$.
At any instant, the part of the rim (of the cylinder) that is at point $P$ is at rest relative to the surface because slipping does not occur.
The figure above shows a timelapse of two points of a rolling cylinder – its centre of mass and one point at its rim.
Decomposition Of Rolling Motion
It is not hard to see that a pure rolling motion is just made up of two components – translation and rotation.
A rolling object with its centre of mass moving at $v_{\text{CM}}$ is just doing a translation with speed $v_{\text{CM}}$ as well as a rotation with $\omega = \frac{v_{\text{CM}}}{R}$.
Kinetic Energy Of A Rolling Object
Consider rotation about the contact point $P$.
From Work, Energy & Power Of Rotating Object, we know that:
$$K = \frac{1}{2} I_{P} \omega^{2}$$
We have to have $I_{P}$. From parallel axis theorem, $I_{P} = I_{\text{CM}} + MR^{2}$. Hence,
$$\begin{aligned} K &= \frac{1}{2} I_{\text{CM}} \omega^{2} + \frac{1}{2} M R^{2} \omega^{2} \\ &= \frac{1}{2} I_{\text{CM}} \omega^{2} + \frac{1}{2} M v_{\text{CM}}^{2} \end{aligned}$$
From the above equation, we can see that the total kinetic energy of an object undergoing rolling motion is the sum of the rotational kinetic energy about its centre of mass and the translational kinetic energy of its centre of mass.