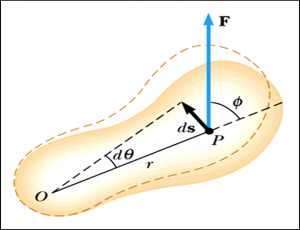
Consider a point rotating through a distance $ds$. Let’s calculate the work done by the force $\vec{F}$.
$$\begin{aligned} dW &= \vec{F}.d\vec{s} \\ &= \left( F \sin{\phi} \right) r \, d \theta \end{aligned}$$
From the definition for torque, we know that $rF \sin{\theta} = \tau$.
Hence,
$$dW = \tau \, d \theta$$
From the equation above, we can see that only the tangential component of $\vec{F}$, which is $F \sin{\theta}$, does work.
The power is given by:
$$\begin{aligned} P &= \frac{dW}{dt} \\ &= \tau \frac{d \theta}{dt} \\ &= \tau \omega \end{aligned}$$
Work & Rotational Energy
Let’s find a way to relate work and rotational energy.
First, we link $\tau$ with $\omega$.
$$\begin{aligned} \tau &= I \alpha \\ &= I \frac{d \omega}{dt} \\ &= I \frac{d \omega}{d \theta} \frac{d \theta}{dt} \\ &= I \frac{d \omega}{d \theta} \omega \end{aligned}$$
Then, using the equation above, we can express $dW$ in terms of $\omega$:
$$\begin{aligned} dW &= \tau \, d \theta \\ &= I \omega \, d \omega\end{aligned}$$
Hence,
$$\begin{aligned} W &= \int\limits_{\theta_{0}}^{\theta} \tau \, d\theta \\ &= I \int\limits_{\omega_{o}}^{\omega} \omega \, d \omega \\ &= \frac{1}{2} I \omega^{2}-\frac{1}{2} I \omega_{0}^{2} \end{aligned}$$
From the above equation, we can see that:
The net work done by external forces in rotating a rigid object about a fixed axis is equal to the change in the object’s rotational energy.
Another result from the above:
The kinetic energy of a rotating object is given by:
$$E_{\text{rot}} = \frac{1}{2} I \omega^{2}$$