A mechanical system moves as if all its mass were concentrated at its centre of mass (CM).
If an external force F acts on this system of total mass M, the centre of mass accelerates at $a = \frac{F}{M}$.
This is independent of other motion, e.g. vibration, rotation of the system.
This provides another way to look at conservation of linear momentum.
Note:
The centre of mass of a homogeneous, symmetric object must lie on an axis of symmetry.
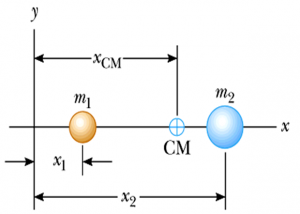
Centre Of Mass Of Two Particles
The centre of mass of two particles is given by:
$$x_{CM} = \frac{m_{1}x_{1} + m_{2}x_{2}}{m_{1}+m_{2}}$$
Centre Of Mass Of A System Of Particles
We can extend the above equation to a system of particles (instead of two particles). We will have:
$$\begin{aligned} x_{CM} &= \frac{m_{1}x_{1} + m_{2}x_{2} + m_{3}x_{3} + \dots + m_{n}x_{n}}{m_{1}+m_{2}+m_{3} + \dots + m_{n}} \\ &= \frac{\sum\limits_{i} m_{i}x_{i}}{\sum\limits_{i} m_{i}} \end{aligned}$$
We can further extend it in the other directions:
$$\begin{aligned} y_{CM} &= \frac{\sum\limits_{i} m_{i}y_{i}}{\sum\limits_{i} m_{i}} \\ z_{cm} &= \frac{\sum\limits_{i} m_{i}z_{i}}{\sum\limits_{i} m_{i}} \end{aligned}$$
Since $\vec{r}_{CM} = x_{CM} \, \hat{i} + y_{CM} \, \hat{j} + z_{CM} \, \hat{k}$, we have:
$$\begin{aligned} \vec{r}_{CM} &= \frac{\sum\limits_{i} m_{i}x_{i} \, \hat{i} + m_{i}y_{i} \, \hat{j} + m_{i}z_{i} \, \hat{k}}{\sum\limits_{i} m_{i}} \\ \vec{r}_{CM} &= \frac{\sum\limits_{i} m_{i} \vec{r}_{i}}{M} \end{aligned}$$
Centre Of Mass Of An Extended Object
In the above treatment, we have been dealing with a system of point particles. Let’s try to find the centre of mass of an extended object (whereby it can be considered to be made up of numerous point particles).
First, we divide the extended object into elements of mass $\Delta m_{i}$, we have:
$$x_{CM} \approx \frac{\sum\limits_{i} x_{i} \, \Delta m_{i}}{M}$$
In the limits where $\Delta m_{i} \rightarrow 0$, we have:
$$\begin{aligned} x_{CM} &= \lim_{\Delta m_{i} \rightarrow 0} \frac{\sum\limits_{i} x_{i} \, \Delta m_{i}}{M} \\ &= \frac{1}{M} \int x \, dm \end{aligned}$$
Similarly, in the other direction,
$$\begin{aligned} y_{CM} &= \frac{1}{M} \int y \, dm \\ z_{CM} &= \frac{1}{M} \int z \, dm \end{aligned}$$
Combining, we have:
$$\vec{r}_{CM} = \frac{1}{M} \int \vec{r} \, dm$$
For a homogeneous (constant density) body that has a geometric centre, the centre of mass is the geometric centre. (E.g. Solid sphere, cube and cylinder)
The centre of mass of any symmetric object lies on an axis of symmetry and on any plane of symmetry.
If $\vec{g}$ is constant over the mass distribution, the centre of gravity coincides with the centre of mass. If an object is hung freely from any point, the vertical line through this point must pass through the centre of mass.
The centre of mass need NOT be within the body itself.