The operation of a rocket depends upon the law of conservation of linear momentum as applied to a system of particles, where the system is the rocket plus the ejected fuel.
Please do not believe the urban folklore that the lift of a rocket is generated by the exhaust gases “pushing” against the ground.
Because the gases are given momentum when they are ejected out of the engine, the rocket receives a compensating momentum in the opposite direction. Therefore, the rocket is accelerated as a result of the “push”, or thrust, from the exhaust gases.
Let’s look in rocket propulsion in more details.
Consider in deep space (zero gravity). The mass of the rocket will be changing due to the ejection of exhaust gases. Please neglect the effects of relativity. Note that $v_{ex}$ is the exhaust speed of gas, which is just the velocity of the exhaust gas relative to the rocket.
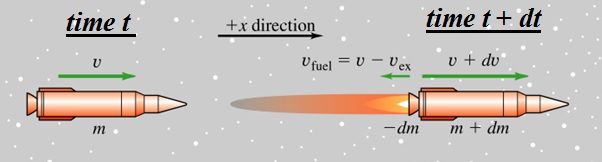
At time t, the mass of the rocket is $m$ and the velocity of rocket is $\vec{v}$.
At time $t + dt$, the mass of the rocket is $m + dm$ (where $dm$ is negative), the velocity of rocket is $v + dv$ and the velocity of gas (in the coordinate system), $v_{\text{fuel}} = v-v_{ex}$
From Conservation of linear momentum, we have:
$$\begin{aligned} mv &= \left( m + dm \right) \left( v + dv \right) + \left( – dm \right) \left( v-v_{ex} \right) \\ mv &= mv + v \, dm + m \, dv + dm \, dv-v \, dm + v_{ex} \, dm \\ m \, dv &=-v_{ex} \, dm-dm \, dv \\ m \frac{dv}{dt} &=-v_{ex} \frac{dm}{dt} \\ a &=-\frac{v_{ex}}{m} \frac{dm}{dt} \end{aligned}$$
We have found the acceleration as shown above. Now, let’s find the $v$.
$$\begin{aligned} m \frac{dv}{dt} &=-v_{ex} \frac{dm}{dt} \\ dv &=-v_{ex} \frac{dm}{m} \\ \int\limits_{v_{i}}^{v_{f}} \, dv^{\prime} &=-\int\limits_{m_{i}}^{m_{f}} \frac{v_{ex}}{m} \, dm \\ \left[ v \right]_{v_{i}}^{v_{f}} &=-v_{ex} \left[ \ln{m} \right]_{m_{i}}^{m_{f}} \\ v_{f}-v_{i} &=-v_{ex} \ln{\left( \frac{m_{f}}{m_{i}} \right) } \end{aligned}$$
From the equation, we can see that in order to have a large final velocity, we will need:
- high exhaust speed
- the ratio $\frac{m_{f}}{m_{i}}$ should be as large as possible
The thrust, force exerted on the rocket by the ejected exhaust gases, is given by:
$$\text{Thrust} = m \frac{dv}{dt} = \Big| v_{ex} \frac{dm}{dt} \Big|$$