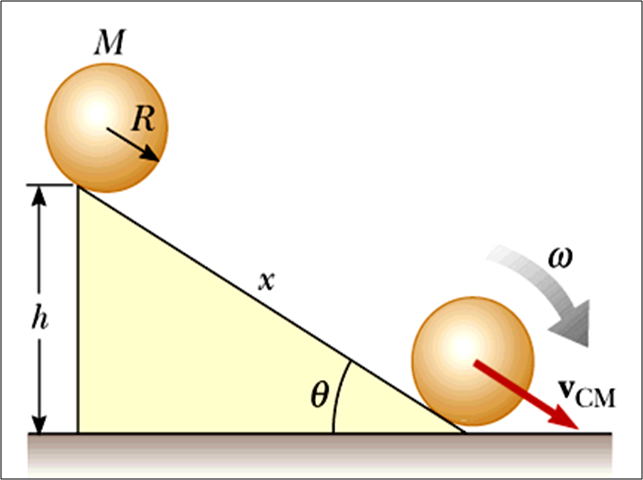
The figure above shows a sphere rolling down an incline. We will analyze this rolling motion.
Important facts about accelerated rolling motion:
- Accelerated rolling motion is possible only if a frictional force is present.
- There is no loss of mechanical energy because the contact point (of the sphere with the ramp) is at rest at any instance.
From the energy conservation equation (Note that $v_{\text{CM}}$ is the velocity of the centre of mass of the sphere at the bottom of the incline.) and using $v_{\text{CM}} = R \omega$, we have:
$$\begin{aligned} E_{\text{kinetic}} = \frac{1}{2} I_{\text{CM}} \omega^{2} + \frac{1}{2} M v_{\text{CM}}^{2} &= Mgh \\ I_{\text{CM}} \frac{v_{\text{CM}}^{2}}{MR^{2}} + v_{\text{CM}}^{2} &= 2gh \\ v_{\text{CM}} &= \sqrt{\frac{2gh}{1 + \frac{I_{\text{CM}}}{MR^{2}}}} \end{aligned}$$
Now, let’s find the acceleration of the centre of mass of the sphere. There are a few methods to do it.
Method 1: Using Energy Conservation Equation
Using the $v_{\text{CM}}$ found above:
We know that the moment of inertia for a solid sphere is $I_{\text{CM}} = \frac{2}{5} MR^{2}$.
Hence,
$$v_{\text{CM}} = \sqrt{\frac{10}{7}gh}$$
For 1D motion with constant acceleration, we have: $v_{\text{CM}}^{2} = 2a_{\text{CM}} x$.
Hence, with $v_{\text{CM}} = \sqrt{\frac{10}{7}gh}$ and $x = \frac{h}{\sin{\theta}}$,
$$a_{\text{CM}} = \frac{5}{7}g \sin{\theta}$$
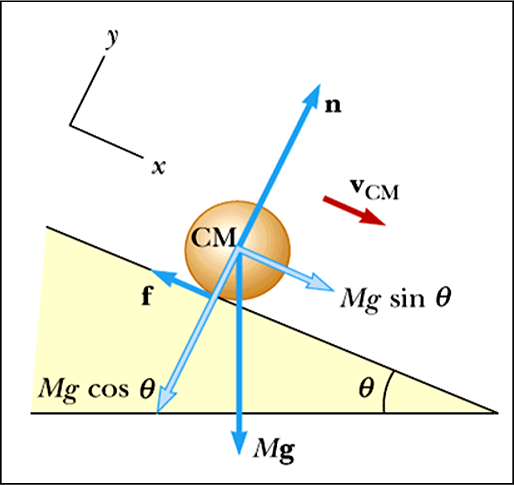
Method 2: Sum Of Forces
From the figure above,
$$\begin{aligned} \sum F_{x} &= Mg \sin{\theta}-f = Ma_{CM} \\ \sum F_{y} &= n-Mg \cos{\theta} = 0 \end{aligned}$$
Let’s calculate the frictional force. The torque about the centre of mass due to the frictional force is given by:
$$\tau_{\text{CM}} = fR$$
Since $\tau_{\text{CM}} = I_{\text{CM}}\alpha$ and $a_{\text{CM}} = R \alpha$, we have:
$$\begin{aligned} f &= I_{\text{CM}} \frac{\alpha}{R} \\ &= I_{\text{CM}} \frac{a_{\text{CM}}}{R^{2}} \\ &= \frac{2}{5} MR^{2} \frac{a_{\text{CM}}}{R^{2}} \\ &= \frac{2}{5} M a_{\text{CM}} \end{aligned}$$
We can substitute the expression for the frictional force into the $\sum F_{x}$ equation. Hence, we have:
$$\begin{aligned} Mg \sin{\theta}-\frac{2}{5} M a_{\text{CM}} &= Ma_{\text{CM}} \\ a_{\text{CM}} &= \frac{5}{7} g \sin{\theta} \end{aligned}$$
Done.
Method 3: Torque Only
Let the point of the sphere in contact with the ramp be point P. Consider the torque about point P:
$$\begin{aligned} \tau_{p} &= I_{p} \alpha \\ MgR \sin{\theta} &= \left( I_{\text{CM}} + MD^{2} \right) \alpha \end{aligned}$$
Since $a_{\text{CM}} = R \alpha$ and using moment of inertia of a sphere and parallel axis theorem, we have:
$$\begin{aligned} MgR \sin{\theta} &= \left( \frac{2}{5} MR^{2} + MR^{2} \right) \frac{a_{\text{CM}}}{R} \\ Mg \sin{\theta} &= \frac{7}{5} M a_{\text{CM}} \\ a_{\text{CM}} &= \frac{5}{7} g \sin{\theta} \end{aligned}$$