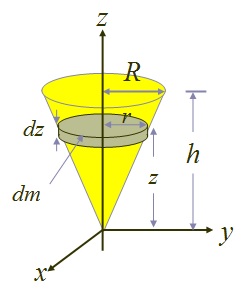
Find the centre of mass of an uniform cone of height $h$ and radius $R$. Let the density of the cone be $\rho$.
It is obvious from the diagram that the x and y components of the centre of mass of a cone is 0:
$$\begin{aligned} x_{CM} &= 0 \\ y_{CM} &= 0 \end{aligned}$$
Hence, we just need to find $z_{CM}$. We will need to use the equation for the centre of mass:
$$z_{CM} = \frac{1}{M} \int z \, dm$$
During the computation, we will need this relation (obtained from similar triangles as seen from the diagram):
$$\frac{r}{z} = \frac{R}{h}$$
We have to find $dm$:
$$\begin{aligned} dm &= \rho \left( \pi r^{2} \right) \, dz \\ &= \rho \pi \frac{R^{2}}{h^{2}} z^{2} \, dz \end{aligned}$$
Then, to find $M$:
$$\begin{aligned} M &= \int \, dm \\ &= \int\limits_{0}^{h} \rho \pi \frac{R^{2}}{h^{2}} z^{2} \, dz \\ &= \rho \pi \frac{R^{2}}{h^{2}} \frac{z^{3}}{3} \Big|_{0}^{h} \\ &= \rho \pi R^{2} \frac{h}{3} \end{aligned}$$
Now, we have enough information to compute $z_{CM}$.
$$\begin{aligned} z_{CM} &= \frac{1}{M} \int z \, dm \\ &= \frac{1}{M} \int\limits_{0}^{h} z \rho \pi \frac{R^{2}}{h^{2}} z^{2} \, dz \\ &= \frac{\rho \pi}{M} \frac{R^{2}}{h^{2}} \frac{z^{4}}{4} \Big|_{0}^{h} \\ &= \frac{3}{\rho \pi R^{2}h} \rho \pi \frac{R^{2}}{h^{2}}\frac{h^{4}}{4} \\ &= \frac{3}{4} h \end{aligned}$$
Next: Motion Of A System Of Particles