Sphere On An Incline
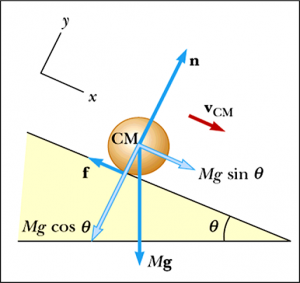
From sphere on an incline, we know that the frictional force and the acceleration of the centre of mass is given by:
$$\begin{aligned} f &= \frac{2}{5} Ma_{\text{CM}} \\ a_{\text{CM}} &= \frac{5}{7} g \sin{\theta} \end{aligned}$$
Combining the two, we have:
$$f = \frac{2}{7} Mg \sin{\theta}$$
If we increase $\theta$ until the frictional force is larger than the static friction force, what will happen?
Since the frictional force is given by $f = \frac{2}{7}Mg \sin{\theta}$ and the static friction force is given by $\mu_{s}n = \mu_{s}Mg \cos{\theta}$, we have the above scenario as:
$$\tan{\theta} > \frac{7}{2} \mu_{s}$$
When $tan{\theta} > \frac{7}{2} \mu_{s}$, the sphere will slide and roll. The velocity and angular velocity will increase but $v_{\text{CM}} \neq R \omega$.
Now, what will happen if $\theta \rightarrow 0$?
When $\theta \rightarrow 0$, $f \rightarrow 0$!
Notice that when $\theta = 0$, the sphere is just rolling on a horizontal surface with $f = 0$. However, contrast this with your everyday knowledge, a rolling ball rolling on a horizontal surface will ultimately stop. What causes this discrepancy?
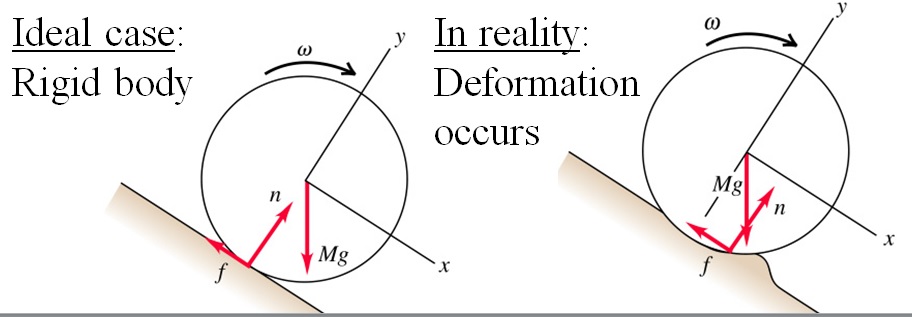
There are several factors causing this discrepancy. There might be other resistive forces such as air resistance or the presence of “rolling friction”.
The “rolling friction” occurs due to this:
During the derivation of the equation for the frictional force, the sphere is assumed to be a rigid body. A rigid body is an idealization, especially for a ball or a rubber-tyred wheel. Deformation occurs, and the wheel rests, not on a single point, but on an area. Sliding occurs on this area of contact, and “normal force” has a small backward component to motion. This is called the rolling friction or tractive resistance.
Rolling Down An Incline
Consider this two scenarios:
- A ball rolls, without sliding, down an incline.
- A box slides down the a frictionless incline, with the same dimensions as the incline above.
Which of them, ball or box, will get to the bottom first?
From sphere on an incline, we know that the acceleration of the centre of mass of ball rolling down an incline is:
$$a_{\text{CM}} = \frac{5}{7}g \sin{\theta}$$
From kinematics, we know that the acceleration of the centre of mass of a box sliding down an incline is:
$$a_{\text{CM}} = g \sin{\theta}$$
Hence, it is obvious that the box will reach the bottom first. Another way to look at the problem: Part of the gravitational potential energy is converted to rotational kinetic energy for the rolling ball. Hence, the kinetic energy of the rolling ball does not increase as fast as the kinetic energy of the sliding box.
Rolling Down Another Incline
Consider this scenario:
Three objects of uniform density – a solid sphere, a solid cylinder, and a hollow cylinder – are placed on top of an incline. They are all released from rest at the same elevation and roll without slipping. Which object will reach the bottom first, and which object will be the last?
In order to solve this problem, we recall that, from the sphere on an incline, the velocity of the centre of mass of the rolling object at the bottom of the incline is given by:
$$v_{\text{CM}} = \sqrt{\frac{2gh}{1 + \frac{I_{\text{CM}}}{MR^{2}}}}$$
Hence, the answer is just a matter of knowing the moment of inertia of the three different objects:
$$\begin{aligned} I_{\text{Cylinder}} &= \frac{1}{2} MR^{2} \\ I_{\text{Sphere}} &= \frac{2}{5} MR^{2} \\ I_{\text{Hollow Cylinder}} &= \frac{1}{2} M \left( R_{1}^{2} + R_{2}^{2} \right) \end{aligned}$$
General Case Of Rolling Motion
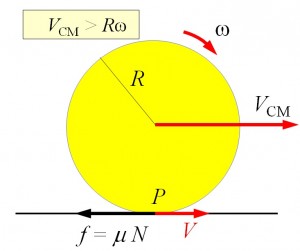
In general, it is not necessary for $v_{\text{CM}}$ to be equal to $R \omega$. When $v_{\text{CM}} > R \omega$, slipping occurs and kinetic friction will act on the rolling object.
When $v_{\text{CM}} > R \omega$,
The equations will be:
$$\begin{aligned} M \frac{d v_{\text{CM}}}{dt} &=-f \\ I \frac{d \omega}{dt} &= fR \end{aligned}$$
Hence, $v_{\text{CM}}$ will decrease and $\omega$ will increase until $v_{\text{CM}} = R \omega$.
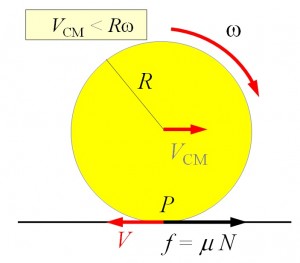
When $v_{\text{CM}} < R \omega$,
The equations will be:
$$\begin{aligned} M \frac{d v_{\text{CM}}}{dt} &=f \\ I \frac{d \omega}{dt} &=-fR \end{aligned}$$
Hence, $v_{\text{CM}}$ will increase and $\omega$ will decrease until $v_{\text{CM}} = R \omega$.
Example: Skidding To Rolling
A uniform sphere rests initially on a level floor. An impulse, delivered horizontally at its centre, gives it a starting speed of $1.0 \text{ ms}^{-1}$ and causes it to skid and roll on the floor. After 0.5 seconds, it stops skidding and start to roll without slipping. Calculate the coefficient of sliding friction due to contact with the floor.
Remember that during skidding, $v_{\text{CM}} \neq R \omega$ because the point of contact is moving.
You can separate the motion of the sphere into translation motion and rotational motion.
For translation motion,
$$\begin{aligned} v &= v_{0}-\frac{\mu_{k}mg}{m}t \\ &= v_{0}-\mu_{k}gt \end{aligned}$$
For rotational motion,
$$\begin{aligned} \tau &= I \alpha \\ \alpha &= \frac{\mu_{k}mg R}{\frac{2}{5}mR^{2}} \\ \alpha &= \frac{5 \mu_{k}g}{2R} \end{aligned}$$
Since $\alpha = \frac{d \omega}{dt}$ and $\omega_{0} = 0$,
$$\omega = \frac{2 \mu_{k}g}{2R}t$$
For a pure rolling motion, $v_{\text{CM}} = R \omega$, hence,
$$\begin{aligned} v_{\text{CM}} &= R \omega \\ v_{0}-\mu_{k}gt &= R \frac{5 \mu_{k} g}{2 R}t \\ v_{0} &= \mu_{k} \frac{7}{2}gt \\ \mu_{k} &= \frac{2 v_{0}}{7gt} \end{aligned}$$
Since the time taken is 0.5 seconds, we have:
$$\mu_{k} = 0.058$$
We’re done!