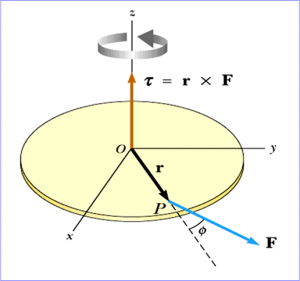
Torque
Recall that torque of a force is:
$$\begin{aligned} \tau &= Fl \\ &= rF \sin{\theta} \end{aligned}$$
Notice that the above is just:
$$\vec{\tau} = \vec{r} \times \vec{F}$$
The direction of the torque is normal to the plane formed by $\vec{r}$ and $\vec{F}$
Angular Momentum
The instantaneous angular momentum $\vec{L}$ of a particle relative to the origin $O$ is defined by the cross product of the instantaneous vector position $\vec{r}$ and its instantaneous linear momentum $\vec{p}$.
$$\vec{L} = \vec{r} \times \vec{p}$$
The SI unit for angular momentum is $\text{kg m}^{2}\text{ s}^{-1}$
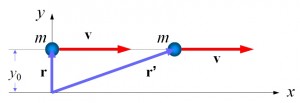
The magnitude and direction of the angular momentum depends on the choice of the origin. This is illustrated in the example below:
Does a particle moving along a straight line have any angular momentum?
From the diagram above, it is obvious that there is no angular momentum:
$$\begin{aligned} \vec{L} &= \vec{r} \times m \vec{v} \\ &= 0 \end{aligned}$$
However, if you change the origin to:
From the diagram above, you can easily tell that the particle possess angular momentum!
$$\begin{aligned} \vec{L} &= \vec{r} \times m \vec{v} \\ &=-y_{0} m v \, \hat{k} \end{aligned}$$
You can take it one step further to show that its angular momentum is conserved:
$$\begin{aligned} \vec{L}^{\prime} &= \vec{r}^{\prime} \times m \vec{v} \\ &=-r^{\prime}mv \sin{\theta} \, \hat{k} \\ &=-y_{0}mv \, \hat{k} \end{aligned}$$
The angular momentum is conserved!
Relation Between Torque & Angular Momentum
From above, we know that:
$$\begin{aligned} \vec{\tau} &= \vec{r} \times \vec{F} \\ &= \vec{r} \times \frac{d \vec{p}}{dt} \end{aligned}$$
We also know that $\vec{L} = \vec{r} \times \vec{p}$, hence,
$$\begin{aligned} \frac{d \vec{L}}{dt} &= \frac{d}{dt} \left( \vec{r} \times \vec{p} \right) \\ &= \vec{r} \times \frac{d \vec{p}}{dt} + \frac{d \vec{r}}{dt} \times \vec{p} \end{aligned}$$
Notice that:
$$\begin{aligned} \frac{d \vec{r}}{dt} \times \vec{p} &= \vec{v} \times v \vec{v} \\ &= 0 \end{aligned}$$
Hence,
$$\frac{d \vec{L}}{dt} = \vec{r} \times \frac{d \vec{p}}{dt}$$
Since $\vec{\tau} = \vec{r} \times \frac{d \vec{p}}{dt}$ (as shown above),
$$\vec{\tau} = \frac{d \vec{L}}{dt}$$
The torque acting on a particle is equal to the time rate of change of the particle’s angular momentum.
This is valid for any origin fixed in an inertial frame.
For a system of particles, we have:
$$\begin{aligned} \vec{L}_{\text{tot}} &= \vec{L}_{1} + \vec{L}_{2} + \dots + \vec{L}_{n} \\ &= \sum\limits_{i = 1}^{n} \vec{L}_{i} \end{aligned}$$
Hence,
$$\begin{aligned} \sum \vec{\tau}_{\text{ext}} &= \sum\limits_{i = 1}^{n} \frac{d \vec{L}_{i}}{dt} \\ &= \frac{d}{dt} \sum\limits_{i=1}^{n} \vec{L}_{i} \\ &= \frac{d \vec{L}_{\text{tot}}}{dt} \end{aligned}$$
The time rate of change of the total angular momentum of the system about some origin in an inertial frame equals the net external torque acting on the system about that origin.
Next: