Let us consider the problem of a particle that is subjected to a linear restoring force F = -kΔx, where Δx is the magnitude of the displacement of the particle from its equilibrium position and k is the force constant. This is an important scenario to consider as the forces between atoms in a solid can be approximated by this kind of interaction.
The total energy of a harmonic oscillator is
E = K + U
$E = \frac{ \left(\Delta p \right)^{2}}{2m} + \frac{1}{2} m \omega ^{2} \left(\Delta x \right)^{2}$
From Heisenberg uncertainty principle, we know that $\Delta x \Delta p \approx \frac{\hbar}{2} = \frac{h}{4 \pi}$ , hence
$E = \frac{h^{2}}{32 m \pi^{2} \left(\Delta x \right)^{2}} + \frac{1}{2} m \omega^{2} \left( \Delta x \right)^{2}$
To find the minimum energy of the system, we minimise E with respect to Δx.
\begin{eqnarray*} \frac{dE}{d \left( \Delta x \right)} &=& 0 \\ – \frac{h^{2}}{16 m \pi^{2} \left(\Delta x \right)^{3}} + m \omega^{2} \left(\Delta x \right) &=& 0 \\ \left(\Delta x \right)^{4} &=& \frac{h^{2}}{16 m^{2} \omega^{2} \pi^{2}} \\ \Delta x &=& \sqrt{\frac{h}{4m \omega \pi}} \end{eqnarray*}
Substituting into the expression for total energy:
$E_{min} = \frac{h \omega}{4 \pi} = \frac{1}{2} \hbar \omega$
This is a very important physical result since it says that the energy of a system described by a harmonic oscillator potential cannot have zero energy. Physical systems such as atoms in a solid lattice or in polyatomic molecules in a gas cannot have zero energy even at absolute zero temperature. The energy of the ground vibrational state is often referred to as “zero point vibration”. The zero point energy is sufficient to prevent liquid helium from freezing at atmospheric pressure, no matter how low the temperature.
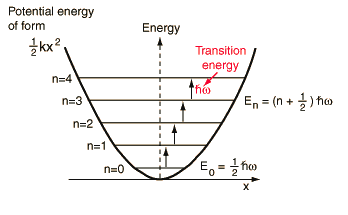
The harmonic oscillator is the foundation for the understanding of complex modes of vibration in larger molecules, the motion of atoms in a solid lattice, the theory of heat capacity, etc. In fact, the energy levels of a harmonic oscillator are quantised. The energy of the state for which the quantum number is n is given by:
$E_{n} = \left( n + \frac{1}{2} \right) \hbar \omega$
As you can see, the ground state which corresponds to the minimum energy level is $\frac{1}{2} \hbar \omega$, where n = 0. Note that the separation between adjacent energy levels are the same and is equal to ħω.