This is a recap of what you have learned in high school and pre-university. If you require more details, you can visit Speed, velocity & acceleration (O Levels) and/or Kinematics (A Levels).
Coordinate Systems
Coordinate systems are required to describe the position of a point in space.
- 1D line: requires one coordinate
- 2D plane: requires two coordinate
- 3D space: requires three coordinate
A coordinate system consists of:
- a fixed reference point O (origin)
- a set of specified axes with scales and labels
- instructions on how to label a point relative to the origin and axes
Displacement In 2D & 3D Motion
The kinematics equations for 2D & 3D motion can be derived by using the vector properties of displacement, velocity and acceleration.
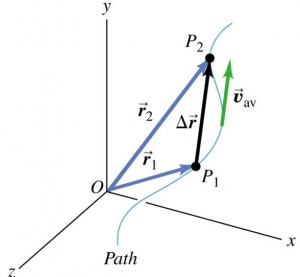
Position vectors $r$, is the vector from origin of the coordinate system O to the point, P.
Displacement is the change of position during the time interval:
$$\Delta \vec{r} = \vec{r}_{2}-\vec{r}_{1}$$
Average velocity:
$$\vec{v}_{\text{avg}} = \frac{\vec{r}_{2}-\vec{r}_{1}}{t_{2}-t_{1}} = \frac{\Delta \vec{r}}{\Delta t}$$
Instantaneous velocity:
$$\vec{v} = \lim_{\Delta \rightarrow 0} \frac{\Delta \vec{r}}{\Delta t} = \frac{d \vec{r}}{dt}$$
Direction of $\vec{v}$ is a tangent to the path at that point in the direction of motion.
Average acceleration:
$$\vec{a}_{\text{avg}} = \frac{\vec{v}_{2}-\vec{v}_{1}}{t_{2}-t_{1}} = \frac{\Delta \vec{v}}{\Delta t}$$
Instantaneous acceleration:
$$\vec{a} = \lim_{\Delta t \rightarrow 0} \frac{\Delta \vec{v}}{\Delta t} = \frac{d \vec{v}}{dt}$$
- Magnitude change of $\vec{v}$ only – 1D motion
- Direction change of $\vec{v}$ only – circular motion
2D Motion With Constant Acceleration
Since acceleration is constant:
$$\begin{aligned} \frac{dv_{x}}{dt} &= a_{x} = \text{constant} \\ \frac{dv_{y}}{dt} &= a_{y} = \text{constant} \end{aligned}$$
we can get (via integration):
$$\begin{aligned} v_{x} &= v_{x, 0} + a_{x} t \\ v_{y} &= v_{y, 0} + a_{y} t \end{aligned}$$
Which is:
$$\vec{v} = \vec{v}_{0} + \vec{a} t$$
Similarly, we can decompose 2D motion into 2 independent motion:
$$\begin{aligned} \frac{d \vec{r}}{dt} &= \vec{v} \\ \frac{dx}{dt} \hat{i} + \frac{dy}{dt} \hat{j} &= v_{x} \hat{i} + v_{y} \hat{j} \end{aligned}$$
You can express the equation above as:
$$\begin{aligned} \frac{dx}{dt} &= v_{x} = v_{x, 0} + a_{x} t \\ \frac{dy}{dt} &= v_{y} = v_{y, 0} + a_{y} t \end{aligned}$$
Integrating the above equations:
$$\begin{aligned} x &= x_{0} + v_{x, 0} t + \frac{1}{2} a_{x} t^{2} \\ y &= y_{0} + y_{y, 0}t + \frac{1}{2} a_{y} t^{2} \end{aligned}$$
The above equations are just:
$$\begin{aligned} \vec{r} &= x \, \hat{i} + y \, \hat{j} \\ &= \vec{r}_{0} + \vec{v}_{0} t + \frac{1}{2} \vec{a} t^{2} \end{aligned}$$
2D motion with constant acceleration is equivalent to 2 independent motions in the x and y directions with constant accelerations $a_{x}$ and $a_{y}$.
Projectile Motion
There are two common assumptions when solving problems for projectile motion:
- Free-fall acceleration
- Neglect air resistance
Projectile motion is the superposition of 2 motions:
- constant horizontal velocity
- vertical free fall
Let’s consider an object whose initial velocity $\vec{v}_{0}$ makes an angle $\alpha_{0}$ with the horizontal. Choosing the y-direction as positive upwards and taking $x_{0} = y_{0} = 0$ at $t = 0$,
The initial velocity in x and y directions:
$$\begin{aligned} v_{0, x} &= v_{0} \cos{\alpha_{0}} \\ v_{0, y} &= v_{0} \sin{\alpha_{0}} \end{aligned}$$
The velocity in terms of the initial velocity will be:
$$\begin{aligned} v_{x} &= v_{0, x} \\ &= v_{0} \cos{\alpha_{0}} = \text{constant} \end{aligned}$$
$$\begin{aligned} v_{y} &= v_{0, y}-gt \\ &= v_{0} \sin{\alpha_{0}}-gt \end{aligned}$$
The displacement is given by:
$$\begin{aligned} x &= v_{0, x} t \\ &= v_{0} t \cos{\alpha_{0}} \end{aligned}$$
$$\begin{aligned} y &= v_{0, y} t-\frac{1}{2} g t^{2} \\ &= v_{0} t \sin{\alpha_{0}}-\frac{1}{2} g t^{2} \end{aligned}$$
Using t in terms of x and substituting that into the above equation for y, we can obtain the trajectory of the form $y = \text{f}\left( x \right)$.
$$y = \left( \tan{\alpha_{0}} \right) x-\left( \frac{g}{2 v_{0}^{2} \cos^{2}{\alpha_{0}}} \right) x^{2}$$
, which is a parabola of the form: $y = ax-bx^{2}$
At the peak of its trajectory, in the vertical direction, $v_{y} = 0$. Using the kinematics equations and solving, we can obtain the maximum height:
$$h = y_{\text{max}} = \frac{v_{0}^{2} \sin^{2}{\alpha_{0}}}{2g}$$
We can use the trajectory formula to calculate the horizontal range. When the projectile reaches the ground, $y = 0$.
$$\begin{aligned} y &= 0 \\ \left( \tan{\alpha_{0}} \right) x-\left( \frac{g}{2 v_{0}^{2} \cos^{2}{\alpha_{0}}} \right) x^{2} &= 0 \\ \left( \tan{\alpha_{0}} \right) &= \left( \frac{g}{2 v_{0}^{2} \cos^{2}{\alpha_{0}}} \right) x \\ R = x &= \frac{v_{0}^{2} \sin{\left( 2 \alpha_{0} \right)}}{g} \end{aligned}$$
From the above equation, we can see that R is at maximum when $\alpha_{0} = 45^{\circ}$.
Uniform Circular Motion
Acceleration occurs when there is a change in magnitude and/or direction of velocity.
Uniform circular motion occurs when there is a change of direction of velocity only. (The object moves at constant speed.)
Time for one revolution, T, is given by: (aka Period)
$$T = \frac{2 \pi R}{v}$$
Centripetal acceleration:
$$\begin{aligned} a_{\text{rad}} &= \frac{v^{2}}{R} \\ &= \frac{4 \pi^{2} R}{T^{2}} \end{aligned}$$
Non-uniform Circular Motion
If the speed is not constant, there will also be a tangential acceleration, equals to the rate of change of speed:
$$\Big| \vec{a}_{t} \Big| = a_{t} = \frac{d \Big| \vec{v} \Big|}{dt}$$
In general, for any motion, where there is a change in the direction and magnitude of velocity, the acceleration is the vector sum of the tangential and radial accelerations:
$$\vec{a} = \vec{a}_{r} + \vec{a}_{t}$$
The tangential acceleration causes the change in the speed of the particle, it is parallel to the instantaneous velocity, and its magnitude is:
$$\Big| \vec{a}_{t} \Big| = a_{t} = \frac{d \Big| \vec{v} \Big|}{dt}$$
The radial acceleration arises from the change in direction of the velocity vector. It is perpendicular to instantaneous velocity and has an absolute magnitude given by:
$$\Big| \vec{a}_{r} \Big| = a_{r} = \frac{v^{2}}{r}$$