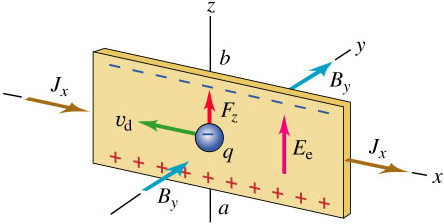
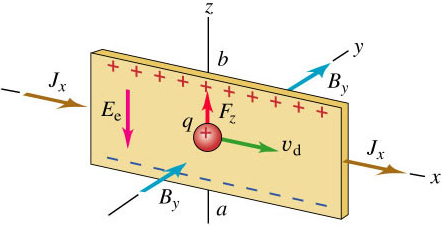
Consider a conductor in the form of a flat strip,
If the charge carriers in the conductor are electrons:
Short overview of what is happening: Initially, the conductor is not polarised. There is a magnetic field incident on the conductor as shown above. Due to the magnetic force experienced by the charge carriers, the charge carriers will be pushed to one end of the conductor. This will result in the conductor being negatively charged at one end and positively charged at the other. The charge carriers will then experience electric force due to the charge accumulation, which will slow down the charge polarization of the conductor. This will continue until the magnetic force is countered by the electric force experienced by the charge carriers.
The magnetic force experienced by the negative charge is:
$$\begin{aligned} \vec{F}_{B} &= q \left( – v_{d} \hat{i} \times B_{y} \hat{j} \right) \\ &= -qv_{d}B_{y} \hat{k} \end{aligned}$$
The electric force experienced by the negative charge is:
$$\vec{F}_{E} = qE_{z} \hat{k}$$
In the steady state,
$$\begin{aligned} \vec{F}_{B} + \vec{F}_{E} &= 0 \\ qv_{d}B_{y} – qE_{z} &= 0 \\ v_{d} = \frac{E_{z}}{B_{y}} \end{aligned}$$
The current density (J) is given by:
$$J = nqv_{d}$$
,where n is the number of charge carriers per unit volume.
Equating that with the equation for $v_{d}$ found above, we have:
$$n = \frac{J_{x}B_{y}}{|q|E_{z}}$$
We can use hall effect to find the number of charge carriers per unit volume. (Since we know J, B, q and E)
Note: The analysis differs slightly for positive charge carriers. But the end result is the same. The analysis for positive charge carriers are shown below.
Magnetic force experienced by positive charge carriers:
$$\begin{aligned} \vec{F}_{B} &= q \left( v_{d} \hat{i} \times B_{y} \hat{j} \right) \\ &= qv_{d}B_{y} \hat{k} \end{aligned}$$
Electric force experienced by positive charge carriers:
$$\vec{F}_{E} = -qE_{z} \hat{k}$$
Next: Magnetic Force On Current Carrying Conductor
Previous: Magnetic Field & Motion Of Charged Particles In Magnetic Fields
Back To Electromagnetism (UY1)