Table of Contents
Atmospheric Pressure
Air is a fluid. We are living at the bottom of a “sea” of air called the atmosphere. The weight of the Earth’s atmosphere pushing down on each unit area of Earth’s surface constitutes the atmospheric pressure.
Origin of Atmospheric Pressure
Atmospheric pressure exists because of molecular bombardment by energetic air molecules. Under normal conditions, there is a large number of air molecules moving at high velocities. This large number of air molecules make frequent collisions with the walls of the container. When the air molecules hit the wall, they rebound from the wall and a force is exerted on the wall from the rebound. The force per unit area exerted by the air molecules on the wall is referred to as the air pressure on the wall. More information on this can be found in Three States of Matter and the subsequent sub-topics.
Atmospheric Pressure At Sea Level
The pressure exerted by this layer of air at sea level is $1.013 \times 10^{5} \, \text{Pa}$. This value is referred to as one atmosphere and is equivalent to placing 1 kg weight on an area of $1 \text{ cm}^{2}$. The pressure at higher altitudes is lower.
Factors Affecting Atmospheric Pressure
Several key factors can cause atmospheric pressure to vary from place to place and over time. Understanding these factors can help us predict weather patterns, plan for outdoor activities, and comprehend the fundamental principles of meteorology.
1. Altitude or Elevation
- Principle: Atmospheric pressure decreases with an increase in altitude. The higher you go, the less air there is above you to exert pressure.
- Impact: This is why mountain tops have lower atmospheric pressure than the Earth’s surface, and it’s also a critical consideration in aviation and mountain climbing.
2. Temperature
- Principle: Warm air expands and rises, leading to lower pressure areas, while cold air is denser, sinks, and creates areas of higher pressure.
- Impact: This relationship between temperature and pressure is fundamental to weather patterns, including the formation of high and low-pressure systems that dictate weather changes.
3. Humidity
- Principle: Moist air (or high humidity) is lighter than dry air because water molecules ($\text{H}_2\text{O}$) have less mass than the nitrogen ($\text{N}_2$) and oxygen ($\text{O}_2$) molecules that make up the bulk of the atmosphere.
- Impact: Regions with higher humidity, such as tropical areas, tend to have lower atmospheric pressure, influencing weather systems and precipitation patterns.
4. Ocean Currents
- Principle: Ocean currents can significantly influence atmospheric pressure over coastal areas. Warm currents can heat the air above them, lowering the air pressure, while cold currents can do the opposite.
- Impact: This can lead to changes in weather and climate in coastal regions, affecting local weather patterns and even contributing to the formation of fog.
5. Gravitational Pull
- Principle: The Earth’s gravity pulls air molecules towards its center, creating atmospheric pressure. The gravitational pull can vary slightly depending on latitude and altitude.
- Impact: Although these variations are minimal, they can affect the distribution of atmospheric pressure around the planet to some extent.
6. Earth’s Rotation
- Principle: The Coriolis effect, resulting from Earth’s rotation, influences wind patterns and ocean currents, which in turn affect atmospheric pressure distributions.
- Impact: This effect causes weather systems to move in particular patterns, such as cyclones spinning in different directions in the Northern and Southern Hemispheres.
Common Measurement Units Of Atmospheric Pressure
- Pascals (Pa): The Pascal is the SI (International System of Units) unit for measuring pressure. It represents the force of one newton per square meter. Due to its small magnitude, atmospheric pressure is often expressed in kilopascals (kPa), where 1 kPa = 1,000 Pa.
- Millibars (mb): Historically popular in meteorology, the millibar is another unit for measuring atmospheric pressure. One millibar equals 100 Pascals or 0.1 kilopascals. The standard atmospheric pressure at sea level is about 1013.25 mb.
- Inches of Mercury (inHg): This unit is derived from the use of mercury in barometers, where atmospheric pressure is measured by the height of a mercury column. Standard atmospheric pressure is equivalent to 29.92 inches of mercury. This unit is commonly used in aviation and meteorology in the United States.
- Atmospheres (atm): The atmosphere is a unit of pressure defined as being equal to the standard atmospheric pressure at sea level. 1 atm is equivalent to 101,325 Pascals, 1013.25 millibars, or 29.92 inches of mercury.
Interconversion Between Units
To convert between these units of atmospheric pressure, you can use the following conversion factors:
- From Pascals to Millibars: Divide the number of Pascals by 100.
- From Millibars to Inches of Mercury: Multiply the number of millibars by 0.02953.
- From Inches of Mercury to Pascals: Multiply the number of inches of mercury by 3,386.389.
- From Atmospheres to Pascals: Multiply the number of atmospheres by 101,325.
Barometer
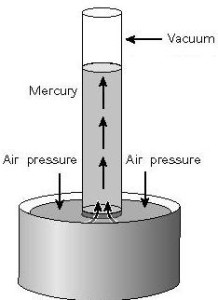
A barometer is a simple instrument for measuring atmospheric pressure.
A barometer can be made by filling up a long glass tube with mercury, then turning it upside down in a bath of mercury as shown. The space at the top of the barometer tube is a vacuum and exerts no pressure on the mercury column.
The atmosphere pushes against the mercury bath, which in turn pushes the mercury up the tube. Hence,
$$\text{Pressure due to mercury column} = \text{Pressure due to atmospheric pressure}$$
The vertical height of the mercury column gives the required atmospheric pressure.
From Hydrostatic Pressure, we know that:
$$\begin{aligned} p_{air} &= p_{\text{mercury column}} \\ &= h \rho g \end{aligned}$$
,where h is the height of mercury column, $\rho$ is density of mercury, g is gravitational acceleration.
Length Of Mercury Column At 1 atmosphere
We can compute the length of the mercury column if 1 atm ($1.013 \times 10^{5} \text{ Pa}$) of atmospheric pressure is acting on the mercury bath. The computation is as follows: (Density of mercury is $13.6 \times 10^{3} \text{kg m}^{-3}$)
$$\begin{aligned} p_{\text{1 atm}} &= \rho g h \\ 1.013 \times 10^{5} &= 13.6 \times 10^{3} \times 9.8 \times h \\ h &= 0.760 \text{ m} \\ h &= 76 \text{ cm} \end{aligned}$$
Barometers of Different Heights & Sizes
The figure above shows barometers of different heights and sizes. Since the principle behind the barometer is the phenomenon of hydrostatic pressure, we know that only the height of the fluid column is important in the determination of the pressure at the bottom. This means that the height, h in the above figure will remain unchanged if:
- the glass tube is lifted up slightly from the dish
- the glass tube is lowered further into the dish
- the diameter of the glass tube increases
- the glass tube is tilted
- the quantity of mercury in the dish is increased.
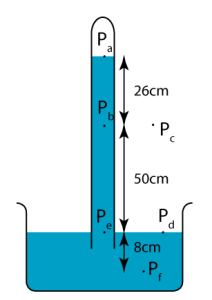
Pressures At Different Heights Of A Barometer
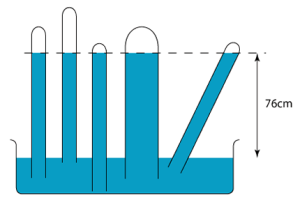
Let’s consider the figure above. We have:
- The pressure at $P_{a}$ is zero. (It is a vacuum in the air gap.)
- The pressure at $P_{b}$ is due to 26 cm of mercury.
- The pressure at $P_{e}$ is due to 76 cm of mercury.
- The pressure at $P_{f}$ is due to 84 cm of mercury.
- Pressure at $P_{b}$ and $P_{c}$ is at atmospheric pressure, i.e. 1 atm. Note: Technically, the pressure at $P_{c}$ is slightly lesser than $P_{b}$.
- Pressure at $P_{d}$ and $P_{e}$ is the same!
Characteristics
- Standard Atmosphere is the mean atmospheric pressure naturally existing at sea level on the surface of the Earth. It is equivalent to the pressure exerted by a vertical column of mercury (as in a barometer) 760 mm high or 101,325 Pa.
- If the mercury is replaced by water, the vertical column of water equivalent to the atmospheric pressure is approximately 10 m.
- The atmosphere pressure does vary from day to day and place to place.
Exploring Barometric Principles With A Shorter Mercury Tube
What happens when we utilize a tube shorter than the conventional length required for creating a vacuum at its top? In this case, the tube is fully filled with mercury, and inverted into a mercury bath.
The Transmission of Atmospheric Pressure Through Mercury
A barometer, at its core, is a device that quantifies atmospheric pressure. The traditional setup, as we’ve discussed, involves inverting a long tube filled with mercury into a bath of the same substance. The vacuum that forms at the top exerts no pressure, allowing the column of mercury to reflect atmospheric pressure by balancing it with the weight of the mercury column.
However, in the case of a shorter tube filled to the brim with mercury and devoid of any vacuum space, the dynamics shift intriguingly. Here, the atmospheric pressure exerted on the mercury’s surface in the open bath is transmitted through the mercury up into the tube. This phenomenon aligns with Pascal’s Law, which posits that pressure applied to a confined fluid at rest is uniformly distributed throughout the fluid. This principle underpins the workings of hydraulic systems and is vividly illustrated in our short-tube barometer scenario.
Hydraulic System Analogy
In a hydraulic system, pressure applied at one point is transmitted undiminished to other parts of the system. Similarly, the atmospheric pressure pushing down on the mercury bath’s surface is equally felt at the base of the mercury-filled tube. This uniform pressure transmission ensures that the pressure at the tube’s base, despite the absence of a vacuum or the traditional mercury column measurement, mirrors the atmospheric pressure exerted on the mercury bath’s surface.
Implications for Teaching Atmospheric Pressure
This experiment serves as a powerful teaching tool, illustrating how atmospheric pressure can be conveyed through mercury in a manner akin to the pressure transmission in hydraulic systems. It underscores the concept that atmospheric pressure is not solely measurable through the height of a mercury column in a vacuum but can also be demonstrated through the transmission of pressure in a fully mercury-filled system.
Worked Examples
Example 1
The diagram shows a simple mercury barometer. Which height is a measure of the atmospheric pressure?
Click here to show/hide answer
Answer: C
Example 2
Instead of using mercury, water can be employed in the barometer. What height (h) would the column reach when water is utilized? (Assume the density of water is 1000 kg/m³, gravitational field strength (g) is 10 N/kg, and atmospheric pressure is 100 kPa.)
Click here to show/hide answer
$$\begin{aligned}P_{\text{atm}} &= h \rho_{\text{water}} g \\ 100 \times 10^{3} \text{ Pa} &= h \times 1000 \text{ kg m}^{-3} \times 10 \text{ N kg}^{-1} \\ h &= 10 \text{ m} \end{aligned}$$
The use of water as the liquid in barometers is not practical due to the necessity of a tube exceeding 10 meters in length.

Great explanation, Whoever wrote this, thank you so much
There is though something i don’t understand.
Suppose i use a shorter barometer tube, lets say for example a 20cm tube filled with mercury. I do the experiment exactly like Toriricelli did, but this time the inverted tube of mercury will stay full to the top, and no vacuum will be created. What would be the pressure then, at all these points?
At point e, is Pe 1atm? The hydrostatic pressure at point e is not 76cm of mercury and yet point e is at the same height as point d and hence they both should have the same pressure which is 1 atm
Hi. For your scenario, the barometer will no longer function as a barometer and instead, it is functioning as a basic hydraulic system. In a basic hydraulic system, pressure is transmitted via the incompressible fluid, mercury in your case. More on hydraulic system here: Hydraulic Systems
In your scenario, the tube is only 20 cm long and is filled with mercury, with no space left for a vacuum to form at the top. This means the tube is shorter than the standard height mercury would naturally fall to under atmospheric pressure (76 cm). Since the open end of the tube is immersed in mercury but exposed to the atmosphere, the pressure at this point (point e) must balance with the atmospheric pressure outside the tube. This is because the atmospheric pressure is pushing down on the mercury in the basin, and this pressure is transmitted through the mercury to the bottom of the tube.
Therefore, the pressure throughout the mercury tube is essentially the atmospheric pressure, much like how pressures are equilibrated in a hydraulic system.