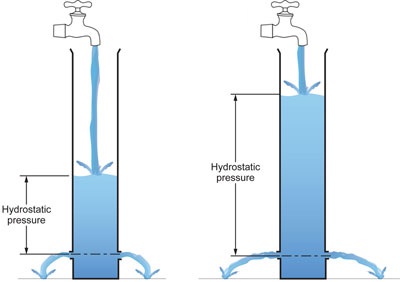
Liquids and gases are called fluids, as they can change their shapes easily. A fluid is a substance that can flow. In the figure above, we notice that the water from the right container is going further than the water from the left container. The only difference between the two container is the height of the water column. Hence, we know that the amount of pressure inside a body of fluids increases with its depth (or height of fluid column).
Pressure Due To Fluid Column
Pressure due to a fluid column (p) = height of column (h) X density of the fluid ($\rho$) X gravitational field strength (g). (The derivation of this formula can be found at the bottom of this post.)
$$p = \rho g h$$
In a fluid, if two points are separated by a vertical height, their difference in pressure is:
$$\Delta p = \rho g \Delta h$$
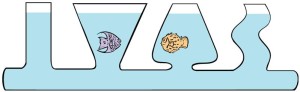
From the formula, $p = \rho g h$, we can see that the pressure depends on the depth and density of the liquid and NOT on the cross-sectional area or volume of the liquid. Hence, the water pressure at the bottom of the container in the figure above will be the same throughout the container as the water level is the same! The shape of the container does NOT matter in the computation of the water pressure!
Properties (Summary)
- Pressure is transmitted throughout the liquid
- Pressure acts in all directions
- All points at the same depth in a fluid are at the same pressure
- Pressure increases with depth
- Pressure is dependent not on the shape of the container but on its depth.
Pressure at Different Depths
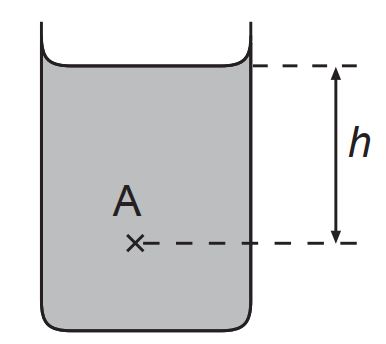
A object immersed in a uniform liquid will experience a pressure which depends only on the height of the liquid above the object.
Hence, consider the picture below.
$$\text{Pressure at point A} = P_{0} + \rho g h$$
, where $P_{0}$ is the atmospheric pressure
Simple derivation of the formula for hydrostatic pressure ($p = \rho g h$):
Consider a column of water occupying a total volume V and a base surface area of A.
The weight of all the water is:
$$W = mg$$
Recall that the mass of the water is just the density of the water X volume of water: $m = \rho V$. Hence,
$$W = \rho V g$$
We note that volume is a product of surface area and height: $V = Ah$
$$W = \rho A h g$$
We recall that formula for pressure: $p = \frac{F}{A}$. Sub. in W into F to give:
$$\begin{aligned} p &= \frac{\rho A h g}{A} \\ &= \rho h g \end{aligned}$$
Done.
