Consider the circuit on the right. Suppose a sinusoidal voltage $V = V_{o} \, sin \, \omega t$ is applied across the resistor of resistance R.
The current in the resistor will be $I = I_{o} \, sin \, \omega t$.
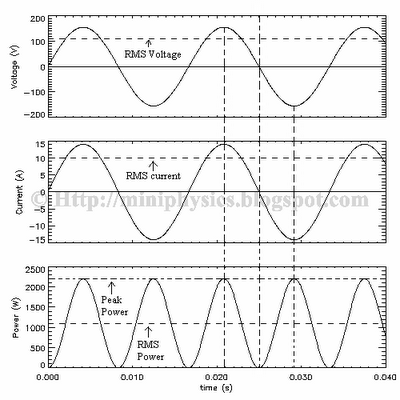
Both the voltage and the current vary sinusoidally with the same angular frequency ω and they are in phase.
The power dissipated by the resistor R at any instant of time is
$\begin{aligned} P & = VI \\ & = (V_{o} \, sin \, \omega t) (I_{o} \, sin \, \omega t) \\ & = V_{o} \, I_{o} \, sin^{2} \, \omega t \\ & = P_{o} \, sin^{2} \, \omega t \end{aligned}$
Maximum power dissipated by the resistor is $P_{o}$ OR Peak Power = $V_{o} \, I_{o}$
Mean power
$$\begin{aligned} \left< P \right> & = \, \left< V_{o} \, I_{o} \, sin^{2} \, \omega t \, \right> \\ & = V_{o} \, I_{o} \, \left< \, sin^{2} \, \omega t \, \right> \\ & = \frac{V_{o} \, I_{o}}{2} \\ & = \frac{1}{2} P_{o} \end{aligned}$$
Mean power is also equal to
$$\begin{aligned} \left< P \right> & = I_{rms}^{2} \, R \\ \left< P \right> & = I_{rms} \, V_{rms} \\ \left< P \right> & = \frac{V_{rms}^{2}}{R} \end{aligned}$$