Table of Contents
Critical Angle
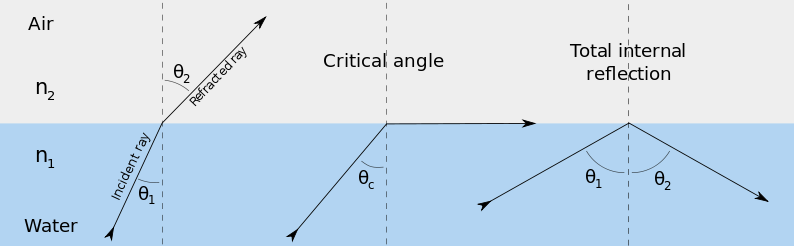
The critical angle is a fundamental concept in optics that applies when light travels from a denser medium to a less dense medium. It is defined as the angle of incidence in the denser medium for which the angle of refraction in the less dense medium is 90 degrees. Beyond this angle, light does not pass into the less dense medium but instead reflects entirely back into the denser medium. The critical angle can only be observed when light moves from a medium with a higher refractive index to one with a lower refractive index (for example, from water to air).
- When the angle of incidence is less than the critical angle, the ray passes out into the less dense medium.
- When the angle of incidence is greater than the critical angle, the ray is reflected back into the denser medium.
The equation relating critical angle, c and the refractive index, n is:
$$\sin{\text{c}} = \frac{1}{n}$$
Short Derivation Of Formula For Critical Angle
Recall that $n_1 \sin(\theta_i) = n_2 \sin(\theta_r)$ and that the light passes from denser ($n_1$) to less dense medium ($n_2 = 1$) – assume air:
$$\begin{aligned} n_1 \sin(\theta_i) &= n_2 \sin(\theta_r) \\ n_{1} \sin \text{c} &= \sin 90^{\circ} \\ n_{1} &= \frac{1}{\sin \text{c}} \\ \sin{\text{c}} &= \frac{1}{n}\end{aligned}$$
Question: Why does the angle of refraction become $90^{\circ}$ and not more at the critical angle?
Answer: This is the limit the light ray can be refracted in air because the angle in air cannot be larger than $90^{\circ}$. When the angle of incidence is greater than the critical angle, all the light undergoes reflection.
Total Internal Reflection
Total internal reflection refers to the complete reflection of a ray of light within an optically-denser medium from the surrounding surfaces of optically less dense media back into the denser medium.
Total Internal Reflection (TIR) is a phenomenon that occurs when a wave (like a light wave) hits the boundary of a denser medium at an angle greater than the critical angle. Instead of refracting into the less dense medium, the wave is completely reflected back into the denser medium. This only happens when light is traveling from a medium with a higher refractive index to one with a lower refractive index.
Conditions For Total Internal Reflection
- The light must travel from a denser medium to a less dense medium.
- The angle of incidence in the denser medium must be greater than the critical angle for that pair of media.
Applications Of Total Internal Reflection
Optical Fibres
Optical fibres are very fine, optically pure glass fibre through which light undergoes total internal reflection to transmit data from one end to the other. Fiber optic technology uses total internal reflection to transmit information across long distances with minimal loss of signal. In a fiber optic cable, light is guided through a core surrounded by a cladding layer; both are made of materials with different refractive indices. The core has a higher refractive index, making it the denser medium. When light signals enter the fiber at a certain angle, they hit the core-cladding boundary at an angle greater than the critical angle. This causes the light to undergo total internal reflection, allowing it to zigzag and travel through the fiber without escaping into the surrounding medium. This principle enables the high-speed transmission of data over the internet and telecommunications networks with much lower loss compared to traditional metal wires.
- Optical fibres usually have polished surfaces coated with a material of suitable refractive index so that there is no loss of light through the sides of the fibre.
- They are used in bundles to transmit light to or receive light from inaccessible places, by repeated totally internal reflections within the fibre.
- Optical fibres are increasingly being used to replace metal telecommunication cables, the messages being encoded as digital pulses of light rather than as fluctuating electric current. They can carry more data and are more reliable.
- Bundles of optical fibres are also used in endoscopes to inspect otherwise inaccessible parts of machines or of the living body.
Cut Diamonds
Diamonds are cut in a way that takes advantage of total internal reflection to maximize their sparkle. Diamonds have a very high refractive index, which means they can have a very small critical angle with air. When light enters a diamond, it is reflected multiple times inside before it exits. Diamond cutters use specific angles and proportions to ensure that as much light as possible is reflected internally and then exits through the top of the diamond to the observer’s eye. This internal bouncing of light, thanks to total internal reflection, creates the brilliant sparkle and fire that diamonds are known for.
Endoscopes & Borescopes
Used in medicine and industrial engineering, these devices rely on total internal reflection to inspect areas that are otherwise inaccessible. Fiber optic bundles within these tools carry light to the target area and then transmit the reflected image back to the observer, allowing for detailed examination without invasive procedures.
Periscopes & Binoculars
TIR is used in the prisms of periscopes and binoculars to reflect light within the device, ensuring that users can see distant objects with clarity. The prisms use total internal reflection to flip the image into the correct orientation and to extend the path of light, providing magnification.
Optical Switches & Sensors
In telecommunications and various sensing applications, total internal reflection can be used to create optical switches that turn signals on or off and sensors that detect changes in the environment. The principle allows for the modulation of light paths based on external conditions, facilitating the control and measurement of optical signals.
Rain Sensors In Vehicles
Some vehicles use rain sensors based on total internal reflection to detect water on the windshield. These sensors emit infrared light that reflects differently when the windshield is wet, triggering the windshield wipers automatically.
Worked Examples
Example 1
Determine the refractive index of diamond given that its critical angle is 24.4 degrees.
Click here to show/hide answer
$$\begin{aligned} \sin{\text{c}} &= \frac{1}{n} \\ \sin 24.4^{\circ} &= \frac{1}{n} \\ n &= 2.42 \end{aligned}$$
Example 2
Determine the refractive index of a transparent material with a critical angle of 35 degrees.
Click here to show/hide answer
$$\begin{aligned} \sin{\text{c}} &= \frac{1}{n} \\ \sin 35^{\circ} &= \frac{1}{n} \\ n &= 1.74 \end{aligned}$$
Example 3
Calculate the critical angle of a transparent material with a refractive index of 1.7.
Click here to show/hide answer
$$\begin{aligned} \sin{\text{c}} &= \frac{1}{n} \\ \sin{\text{c}} &= \frac{1}{1.7} \\ \text{c} &= 36.0 ^{\circ} \end{aligned}$$
Example 4: Understanding Critical Angle
Suppose you are conducting an experiment where you shine a light from water into air at various angles of incidence. If the refractive index of water is 1.33 and that of air is approximately 1.00, calculate the critical angle for this water-air interface. Explain why, at angles greater than this critical angle, you observe total internal reflection.
Click here to show/hide answer
To find the critical angle, we use the formula for the critical angle, which relates the refractive indices of the two media:
$$\sin(c) = \frac{n_2}{n_1}$$
where $c$ is the critical angle, $n_1$ is the refractive index of the denser medium (water, 1.33), and $n_2$ is the refractive index of the less dense medium (air, 1.00). Rearranging and solving for $c$, we get:
$$c = \arcsin\left(\frac{1.00}{1.33}\right) \approx 48.08^{\circ}$$
Beyond this angle, light does not refract into the air but instead reflects entirely back into the water. This is because at angles greater than the critical angle, the law of refraction cannot be satisfied, leading to total internal reflection within the water.
Example 5: Application in Optical Fibres
Describe how the principle of total internal reflection is used in optical fibers to transmit data. Why is it important that the light enters the fiber at an angle greater than the critical angle?
Click here to show/hide answer
Optical fibers utilize the principle of total internal reflection to transmit data efficiently over long distances. These fibers are made of a core surrounded by a cladding, each with different refractive indices. The core has a higher refractive index, acting as the denser medium. When light signals enter the fiber at an angle greater than the critical angle, they hit the core-cladding boundary and undergo total internal reflection. This allows the light to zigzag through the fiber without escaping, minimizing signal loss. It is crucial for the light to enter at an angle greater than the critical angle to ensure that total internal reflection occurs, allowing for the efficient transmission of data.
Example 6: Real-World Phenomena
Explain how the phenomenon of total internal reflection contributes to the “sparkle” seen in diamonds and why diamonds must be cut in a specific way to maximize this effect.
Click here to show/hide answer
The “sparkle” in diamonds is significantly enhanced by total internal reflection. Diamonds have a very high refractive index, which means they have a small critical angle. When light enters a diamond, if it strikes the internal surfaces at angles greater than the critical angle, it undergoes total internal reflection multiple times before eventually exiting the diamond. This multiplicity of reflections and the dispersion of light into its spectral components create the sparkling effect. Diamonds must be precisely cut to ensure that light entering the gem does so at angles that favor total internal reflection within the diamond, maximizing the sparkle by efficiently directing light through and out of the top of the diamond.
Example 7: Critical Thinking on Refractive Indices
Consider a situation where light travels from a medium with a refractive index of 1.5 to another medium with a refractive index of 1.2. Calculate the critical angle for this interface. Discuss the implications if the second medium’s refractive index were to increase slightly, approaching that of the first medium.
Click here to show/hide answer
To calculate the critical angle for light traveling from a medium with a refractive index of 1.5 to one with 1.2, we use the formula:
$$sin(c) = \frac{n_2}{n_1} = \frac{1.2}{1.5}$$
$$c = \arcsin\left(\frac{1.2}{1.5}\right) \approx 53.13^{\circ}$$
If the refractive index of the second medium were to increase, approaching that of the first medium, the critical angle would increase as well, moving closer to 90 degrees. This change means that light could strike the interface at a wider range of angles without undergoing total internal reflection. The phenomenon would become less pronounced as the difference between the refractive indices decreases, indicating a narrower range of conditions under which total internal reflection occurs, potentially affecting the efficiency of applications relying on this principle, such as optical fibers.