Velocity Selector

Recall from Motion of a moving charge in an uniform magnetic field that a moving charge travelling at a speed of v within an uniform magnetic field will experience a force given by:

$$F = Bqv$$

In addition, the force will be always perpendicular to the direction of travel of the charge.

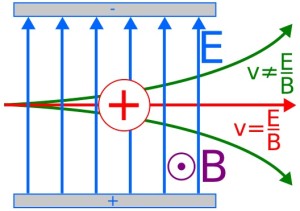
This principle is exploited in an equipment called – Velocity selector, which is shown in the figure below.

In a velocity selector, charged particles must move at a speed of $v = \frac{E}{B}$ in order to pass through the equipment. Hence, a velocity selector, as it’s name implies, allows charged particles with a certain velocity to pass through (hence, selecting particles of a certain velocity). The mechanism of a velocity selector is illustrated below.

The velocity selector will have the following fields:

• An uniform electric field, which is generated by a positively charged bottom plate and negatively charged top plate. This will cause an electric field to form between the plate, that is pointing in the upwards direction.
• An uniform magnetic field throughout the space between the two charged plates. The uniform magnetic field can be directed inwards (into the paper) or outwards (out of the paper). In the figure above, the magnetic field is directed outwards.

When a charged particle (e.g. a positively charged) enters the velocity selector, it will experience forces due to the electric and magnetic field.

• The particle will experience a upwards force due to the electric field (given by $F = qE$)
• The particle will experience a downwards force due to it’s motion through the magnetic field (given by $F = Bqv$). You can use the Flemings’ Left Hand Rule to obtain the direction of the force on the charged particle due to the uniform magnetic field.

In order for the charged particle to pass through the space WITHOUT being deflected (either upwards or downwards), the upwards force must be equal to the downwards force (cancel each other out).

Hence, we have:

$$\begin{aligned} qE &= Bqv \\ v &= \frac{E}{B} \end{aligned}$$

If the positively charged particle has a slightly larger velocity than $\frac{E}{B}$, the particle will be deflected downwards due to the larger downwards force (given by $f = Bqv$).