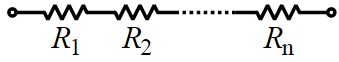Table of Contents
In many situations, several electrical devices are connected to the same power supply. There are two basic methods of connecting resistors or other devices together. They are called series and parallel connections.
The derivation of the formula for effective resistance for series and parallel resistors can be found at the end of this post.
Effective Resistance Of Resistors
Resistors In Series
If individual resistors are connected from end to end, the resistors are said to be connected in series. The effective resistance, R, of three resistors of resistances R1, R2; and R3 connected in series (shown in the figure) is given by:
$ R = R_{1} + R_{2} + R_{3}$
In general, if there are n resistors in series, the effective resistance R is given by:
$ R = R_{1} + R_{2} + …. + R_{n}$
Note: In a series connection, the effective resistance, R, is always larger than the largest of the individual resistances.
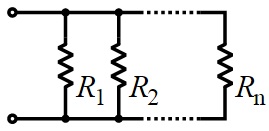
Resistors In Parallel
If each end of individual resistors are connected together to one another as one, the resistors are said to be connected in parallel.
The effective resistance, R, of three resistors of resistances R1, R2 and R3 connected in parallel is given by:
$ \frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}}$
In general, if there are n resistors in parallel, the effective resistance R is given by:
$ \frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + …. + \frac{1}{R_{n}}$
Note: In a parallel connection, the effective resistance, R, is always smaller than the smallest of the individual resistances.
Derivation Of Effective Resistance For Series & Parallel Resistors
Series Resistors
When the resistors are in series, the current through each resistor is the same. We shall denote the current as I. Each resistor will have its own voltage. If the resistance of the resistors are different ($R_{1} \neq R_{2} \neq R_{3} \neq \dots$), the voltage drop across each resistor will be different ($V_{1} \neq V_{2} \neq V_{3} \neq \dots$).
We know that resistance is given by $R = \frac{V}{I}$.
Hence the effective resistance of the whole stretch of resistor is given by:
$$R_{eff} = \frac{V_{total}}{I}$$
However, we know that
$$V_{total} = V_{1} + V_{2} + V_{3} + \dots$$
Substitute that into the effective resistance equation, we have:
$$\begin{eqnarray} R_{eff} &=& \frac{V_{total}}{I} \\ &=& \frac{V_{1} + V_{2} + V_{3} + \dots}{I} \\ &=& \frac{V_{1}}{I} + \frac{V_{2}}{I} + \frac{V_{3}}{I} + \dots \\ &=& R_{1} + R_{2} + R_{3} + \dots \end{eqnarray}$$
Parallel Resistors
When the resistors are in parallel, the voltage drop across each resistor is the same. We shall denote the voltage as V. Each resistor will have its own voltage. If the resistance of the resistors are different ($R_{1} \neq R_{2} \neq R_{3} \neq \dots$), the current through each resistor will be different ($I_{1} \neq I_{2} \neq I_{3} \neq \dots$).
We know that resistance is given by $R = \frac{V}{I}$.
Hence the effective resistance of the whole stretch of resistor is given by:
$$R_{eff} = \frac{V}{I_{total}}$$
However, we know that
$$I_{total} = I_{1} + I_{2} + I_{3} + \dots$$
Substitute that into the effective resistance equation, we have:
$$\begin{eqnarray} R_{eff} &=& \frac{V}{I_{total}} \\ R_{eff} &=& \frac{V}{I_{1} + I_{2} + I_{3} + \dots} \\ \frac{1}{R_{eff}} &=& \frac{I_{1} + I_{2} + I_{3} +\dots}{V} \\ \frac{1}{R_{eff}} &=& \frac{I_{1}}{V} + \frac{I_{2}}{V} + \frac{I_{3}}{V} + \dots \\ \frac{1}{R_{eff}} &=& \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + \dots \end{eqnarray}$$