Metallic conductors at constant temperature
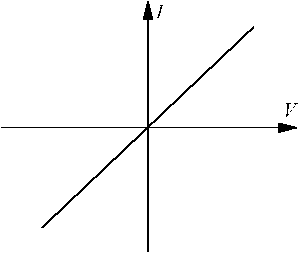
The I-V graph of metallic conductor is a straight line pass through the origin. They obey Ohm’s Law, having resistance that is independent of current. (Ohmic conductors)
Reason: Resistance in metal is the reduction of the drift velocity of electrons due to collision with the lattice ions. If the temperature of the conductor is kept constant, the magnitude of the vibration of the lattice ions remain the same, and hence it’s resistance would remain the same.
