Table of Contents
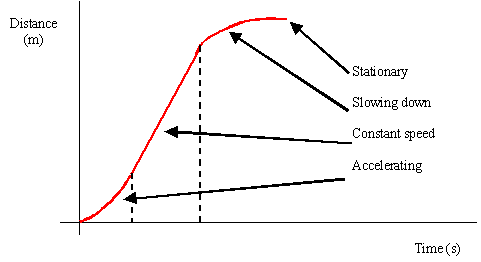
Distance-Time Graphs
- For a distance-time graph, the distance never decreases.
- When the object is stationary, the distance-time graph will be horizontal.
- The gradient of a distance-time graph is the instantaneous speed of the object.
- For straight line with positive gradient, it means that the object is travelling at uniform speed
- There is no straight line with negative gradient (as the distance never decreases)
- For curves, it means that the object is travelling at non-uniform speed
Displacement-Time Graphs
- The details are similar as distance-time graphs, except that the distance is now displacement, and speed is now velocity.
- The gradient of a distance-time graph is the instantaneous velocity of the object.
- One minor difference: There is a straight line with negative gradient, it means that the object is travelling at uniform velocity in the opposite direction.
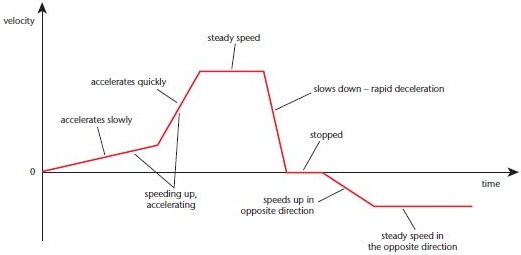
Velocity-Time Graphs
- When the object is stationary, it is a straight horizontal line at 0.
- When the object is undergoing uniform motion, it is a straight horizontal line at $v \, \text{m s}^{-1}$, where v is the velocity of the object.
- The gradient of a velocity-time graph of an object gives the acceleration of the object.
- For straight line with positive gradient, it means that the object is accelerating.
- For straight line with negative gradient, it means that the object is decelerating.
- For curves, it means that the acceleration of the object is changing.
- The area under the graph is the change in the displacement of the object.
Acceleration-Time Graphs
- Area under graph is the change in the velocity of the object
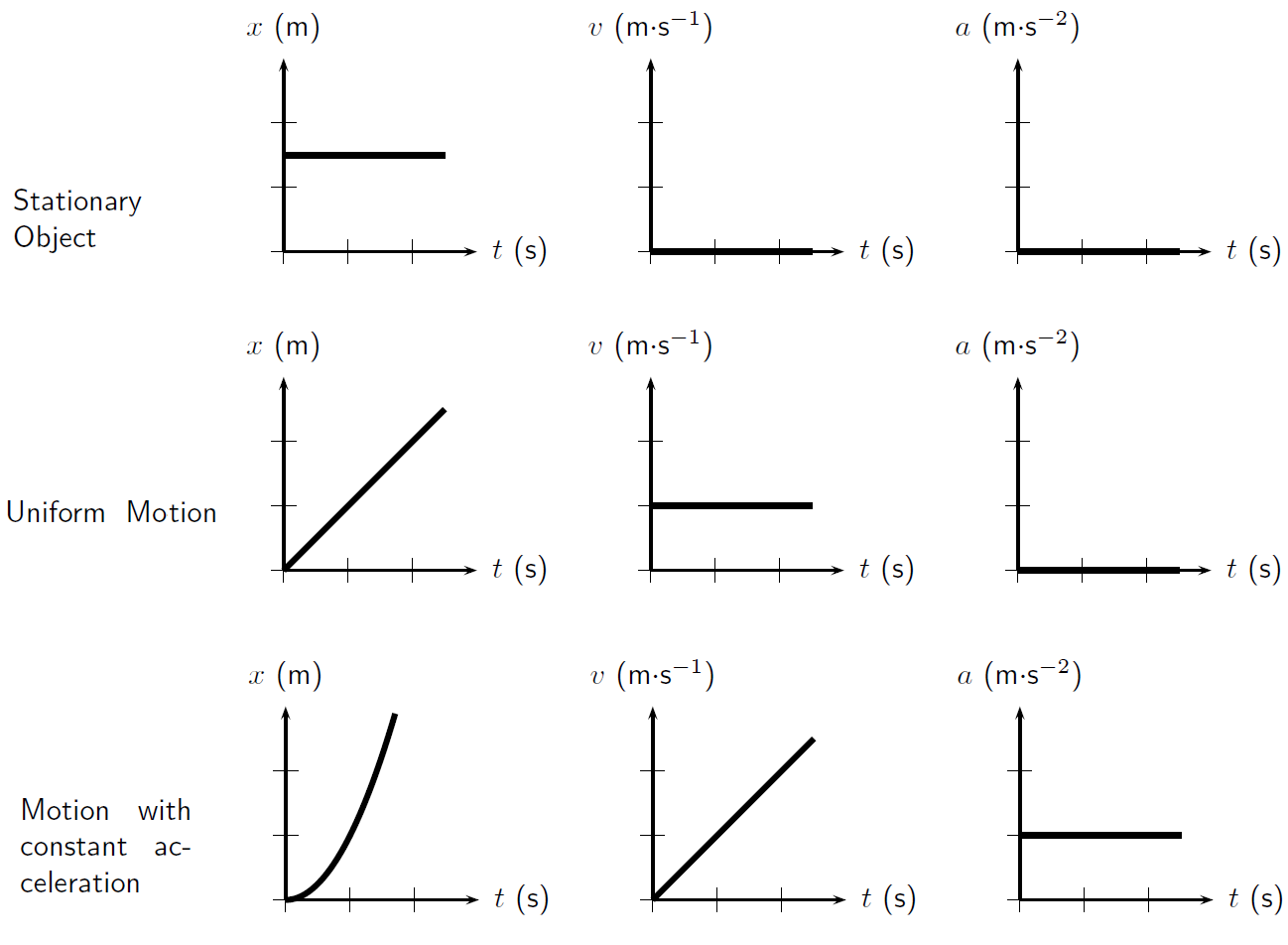
Summary of Kinematics Graphs
The figure below shows the displacement-time graph, velocity-time graph and acceleration-time graph for the respective state of motion. It serves as a summary of the text above.
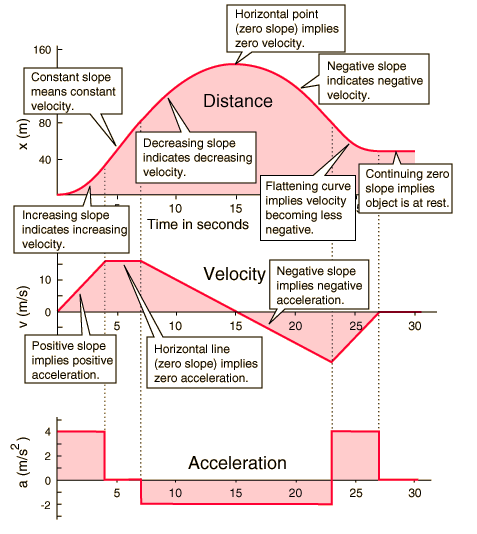
The figure below shows the relationship between displacement-time graph, velocity-time graph and acceleration-time graph.
Worked Examples
Example 1
Can you tell from a displacement-time graph whether an object is stationary?
Click here to show/hide answer
Yes. If the object is stationary, it will appear as a horizontal line on a displacement-time graph.
Example 2
How can you obtain the average velocity and instantaneous velocity from a displacement-time graph.
Click here to show/hide answer
The average velocity can be found by using $\frac{\text{total displacement}}{\text{total time taken}}$.
The instantaneous velocity at a point in time can be found from the gradient of the tangent to that point in time.
Example 3
Can you tell from a velocity-time graph whether an object is stationary?
Click here to show/hide answer
Yes. If the object is stationary, the velocity-time graph will be a horizontal line at $\text{v}=0$.
Example 4
How would you obtain the acceleration of an object from a velocity-time graph? What does the area under a velocity-time graph represent?
Click here to show/hide answer
The acceleration of an object at a point in time can be obtained from the gradient of the tangent to that point in time.
The area under a velocity-time graph represents the total distance traveled.
Example 5
Can you tell from an acceleration-time graph whether an object is stationary?
Click here to show/hide answer
No, you cannot. Do you know why?
Hint: Refer to the summary of Kinematics graphs (located above).
Drop a comment below if you cannot figure out the answer.
Example 6
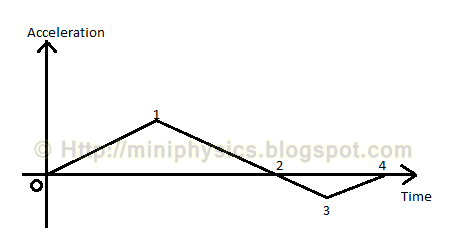
The acceleration-time graph of an object moving in a straight line is as shown. The object started its motion from rest.
At which point is the body moving with the largest speed?
Click here to show/hide answer
Area under acceleration-time graph = change in velocity of the object. At point 2, the area under the graph is the largest.
Answer: 2