It has been found experimentally that electrical resistivity of a metal is related linearly to temperature according to the formula:
$$\rho = \rho_{0} \left[ 1 + \alpha \left( T + T_{0} \right) \right]$$
where ρ is the resistivity at some temperature T (in °C), ρ0 is the resistivity at some reference temperature T0 (usually taken to be 20°C), and α is the temperature coefficient of resistivity.
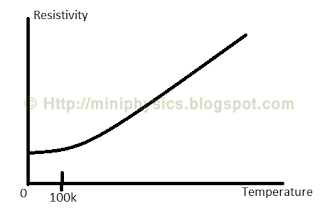
The diagram above shows that above about 100K, the resistivity of a metal increases linearly with temperature even though the Drude model suggests it should increase according to $T_{\frac{1}{2}}$.
Drude model is even worse at explaining the low-temperature resistivities of very pure forms of metals. The resistivity of very pure copper, for example, decreases by a factor of 1000 or more when it is cooled to very low temperatures. These extremely low resistivities imply mean free paths greater than 10-6 m, about 400 times greater than the spacing between ions. We conclude that, although Drude’s theory can describe the flow of electricity through metals in accordance with Ohm’s law, it cannot explain the very long mean free paths of electrons or the measured temperature variation of electrical resistivities.
Furthermore, it is found that the very small low-temperature resistivities found for very pure metals are increased dramatically for samples containing quite small levels of impurities and Drude’s model has no explanation for this.
It turns out that only those electrons close to the Fermi level can be scattered and then only by defects or because of the thermal vibration of the positive ions. This is because the electrons ought to be modelled as waves. In a perfect crystal, electron waves can only be scattered by reflections from planes of atoms when Bragg’s law is satisfied but only a tiny proportion of electron waves satisfy this condition. The electron wave model therefore predicts that electrons travel through a perfect lattice without any significant amount of scattering. Electrons can scatter off defects, however, which is temperature independent. Also, the vibration of the positive lattice ions increases with temperature and this causes thermal scattering of electrons.
At temperatures below about 50 K, the thermal scattering is negligible and the resistivity is determined by defect scattering alone. Beacuse the defect density is independent of temperature, the resistivity is constant in this region. At temperatures above about 50K, the thermal agitation of the lattice becomes important and so the resistivity rises linearly with increasing temperature due to thermal scattering.
Overall, the net electrical resistivity of a metal can thus be described by:
ρ = ρL + ρi, where
ρL is the resistivity caused by the thermal lattice ions,
ρi is the resistivity caused by scattering of the electron waves by the static defects that disturb the uniformity of the lattice.
Note: ρL is independent of the number of defects when their concentration is small, and ρi is independent of temperature.
This wave model has its own limitations, however. For example, it cannot explain why some solids are insulators. There is nothing in the model that can explain why carbon’s four valence electrons are not free to conduct electricity in diamond (an insulator). Also, it does not explain the anomalous Hall effect, why some metals like zinc, cadmium and iron show a Hall effect with the opposite polarity.